Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: =>1/2x=7/2-2/3=21/6-4/6=17/6
=>x=17/3
b: =>2/3:x=-7-1/3=-22/3
=>x=2/3:(-22/3)=-1/11
c: =>1/3x+2/5x-2/5=0
=>11/15x=2/5
hay x=6/11
d: =>2x-3=0 hoặc 6-2x=0
=>x=3/2 hoặc x=3

a: =>x-3/4=1/6-1/2=1/6-3/6=-2/6=-1/3
=>x=-1/3+3/4=-4/12+9/12=5/12
b: =>x(1/2-5/6)=7/2
=>-1/3x=7/2
hay x=-21/2
c: (4-x)(3x+5)=0
=>4-x=0 hoặc 3x+5=0
=>x=4 hoặc x=-5/3
d: x/16=50/32
=>x/16=25/16
hay x=25
e: =>2x-3=-1/4-3/2=-1/4-6/4=-7/4
=>2x=-7/4+3=5/4
hay x=5/8

a: =>2x-1=-2
=>2x=-1
hay x=-1/2
b: \(\Leftrightarrow\left[{}\begin{matrix}3x+2=0\\-\dfrac{2}{5}x-7=0\end{matrix}\right.\Leftrightarrow x\in\left\{-\dfrac{2}{3};-\dfrac{35}{2}\right\}\)
c: x/8=9/4
nên x/8=18/8
hay x=18
d: \(\Leftrightarrow\left(x-3\right)^2=36\)
=>x-3=6 hoặc x-3=-6
=>x=9 hoặc x=-3
e: =>-1,7x=6,12
hay x=-3,6
h: =>x-3,4=27,6
hay x=31
a) \(\dfrac{1}{3}\div\left(2x-1\right)=\dfrac{-1}{6}\)
\(\left(2x-1\right).\dfrac{1}{3}\div\left(2x-1\right)=\left(2x-1\right)\left(-\dfrac{1}{6}\right)\)
\(\dfrac{1}{3}=\left(2x-1\right)\left(-\dfrac{1}{6}\right)\)
\(\dfrac{1}{3}=-1\left(2x-1\right)\div6\)
\(\dfrac{1}{3}=-2x+1\div6\)
\(x=-\dfrac{1}{2}\)
b) \(\left(3x+2\right)\left(\dfrac{-2}{5}x-7\right)=0\)
\(TH1:3x+2=0\)
\(3x=0-2\)
\(3x=-2\)
\(x=\dfrac{-2}{3}\)
\(TH2:\left(-\dfrac{2}{5}x-7\right)=0\)
\(\left(\dfrac{-2}{5}x-7\right)=0\)
\(\left(\dfrac{-2x}{5}+\dfrac{5\left(-7\right)}{5}\right)=0\)
\(\left(\dfrac{-2x-35}{5}\right)=0\)
\(-2x-35=0\)
\(-2x=0+35\)
\(x=-\dfrac{35}{2}\)
c) \(\dfrac{x}{8}=\dfrac{9}{4}\)
\(\Leftrightarrow x=\dfrac{9.8}{4}=\dfrac{72}{4}=18\)
\(x=18\)
d) \(\dfrac{x-3}{2}=\dfrac{18}{x-3}\)
\(x-3=18+2\)
\(x=20-3\)
\(x=17\)
e) \(4,5x-6,2x=6,12\)
\(\dfrac{9x}{2}-6,2.x=6,12\)
\(\dfrac{9x}{2}+\dfrac{-31x}{5}=6,12\)
\(\dfrac{5.9x}{10}+\dfrac{2\left(-31\right)x}{10}=6.12\)
\(\dfrac{45x-62x}{10}=6.12\)
\(=-17x\div10=6.12\)
\(-17x=10.6.12\)
\(x=-3,6\)
h) \(11,4-\left(x-3,4\right)=-16,2\)
\(x-3,4=-16,2+11,4\)
\(x-3,4=-4,8\)
\(x=-1,4\)

a) \(\left(x-\dfrac{1}{2}\right)\left(-3-\dfrac{x}{2}\right)=0\)
Th1 : \(x-\dfrac{1}{2}=0\)
\(x=0+\dfrac{1}{2}\)
\(x=\dfrac{1}{2}\)
Th2 : \(-3-\dfrac{x}{2}=0\)
\(\dfrac{x}{2}=-3\)
\(x=\left(-3\right)\cdot2\)
\(x=-6\)
Vậy \(x\) = \(\left(\dfrac{1}{2};-6\right)\)
b) \(x-\dfrac{1}{8}=\dfrac{5}{8}\)
\(x=\dfrac{5}{8}+\dfrac{1}{8}\)
\(x=\dfrac{3}{4}\)
c) \(-\dfrac{1}{2}-\left(\dfrac{3}{2}+x\right)=-2\)
\(\dfrac{3}{2}+x=-\dfrac{1}{2}-\left(-2\right)\)
\(\dfrac{3}{2}+x=\dfrac{3}{2}\)
\(x=\dfrac{3}{2}-\dfrac{3}{2}\)
\(x=0\)
d) \(x+\dfrac{1}{3}=\dfrac{-12}{5}\cdot\dfrac{10}{6}\)
\(x+\dfrac{1}{3}=-4\)
\(x=-4-\dfrac{1}{3}\)
\(x=-\dfrac{13}{3}\)

c: Ta có: \(\dfrac{1}{3}-\dfrac{7}{8}x=\dfrac{1}{4}\)
\(\Leftrightarrow x\cdot\dfrac{7}{8}=\dfrac{1}{12}\)
\(\Leftrightarrow x=\dfrac{1}{12}\cdot\dfrac{8}{7}=\dfrac{2}{21}\)
d: Ta có: \(\dfrac{3}{2}x+\dfrac{1}{7}=\dfrac{7}{8}\cdot\dfrac{64}{49}\)
\(\Leftrightarrow x\cdot\dfrac{3}{2}=1\)
hay \(x=\dfrac{2}{3}\)

\(a.x+\dfrac{1}{6}=-\dfrac{3}{8}\)
\(\Leftrightarrow x=-\dfrac{13}{24}\)
\(b.2-\left(\dfrac{3}{4}-x\right)=\dfrac{7}{12}\)
\(\Leftrightarrow2-\dfrac{3}{4}+x=\dfrac{7}{12}\)
\(\Leftrightarrow x=-\dfrac{2}{3}\)
\(c.\dfrac{1}{2}x+\dfrac{1}{8}x=\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{5}{8}x=\dfrac{3}{4}\)
\(\Leftrightarrow x=\dfrac{6}{5}\)
\(d.75\%-1\dfrac{1}{2}+0,5:\dfrac{5}{12}-\left(\dfrac{-1}{2}\right)^2\)
\(=\dfrac{75}{100}-\dfrac{3}{2}+\dfrac{1}{2}:\dfrac{5}{12}-\dfrac{1}{4}\)
\(=-\dfrac{3}{4}+\dfrac{6}{5}-\dfrac{1}{4}\)
\(=\dfrac{1}{5}\)
a) \(x+\dfrac{1}{6}=\dfrac{-3}{8}\)
\(x=\dfrac{-3}{8}-\dfrac{1}{6}\)
\(x=\dfrac{-13}{24}\)
vậy x =....
b) \(2-\left(\dfrac{3}{4}-x\right)=\dfrac{7}{12}\)
\(\dfrac{3}{4}-x=2-\dfrac{7}{12}\)
\(\dfrac{3}{4}-x=\dfrac{17}{12}\)
\(x=\dfrac{3}{4}-\dfrac{17}{12}\)
\(x=\dfrac{-2}{3}\)
vậy x =....

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 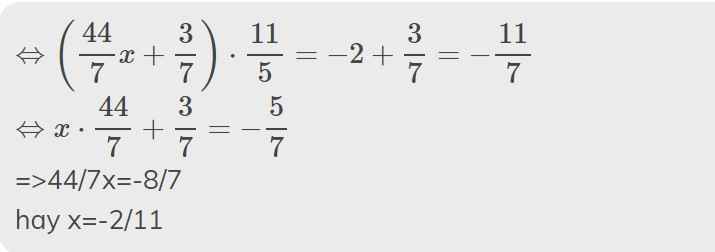
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)
A. 3/5
B. 2/8
C. 2
HT
a) \(\frac{3}{8}-\frac{1}{6}x=\frac{1}{4}\)
\(\frac{1}{6}x=\frac{3}{8}-\frac{1}{4}\)
\(\frac{1}{6}x=\frac{1}{8}\)
\(x=\frac{1}{8}\div\frac{1}{6}\)
\(x=\frac{3}{4}\)
Vậy \(x=\frac{3}{4}\)
b) \(\left(x-1\right)^2=\frac{1}{4}\)
\(\left(x-1\right)^2=\left(\pm\frac{2}{4}\right)^2\)
TH1:
\(\left(x-1\right)^2=\frac{2}{4}^2\)
\(x-1=\frac{2}{4}\)
\(x-1=\frac{1}{2}\)
\(x=\frac{1}{2}+1\)
\(x=\frac{3}{2}\)
TH2:
\(\left(x-1\right)^2=\left(-\frac{2}{4}\right)^2\)
\(x-1=-\frac{2}{4}\)
\(x=-\frac{2}{4}+1\)
\(x=\frac{1}{2}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=\frac{1}{2}\end{cases}}\)
c) \(\left(x-\frac{-1}{2}\right).\left(x+\frac{1}{3}\right)=0\)
TH1:
\(x-\frac{-1}{2}=0\)
\(x=0+\frac{-1}{2}\)
\(x=\frac{-1}{2}\)
TH2:
\(x+\frac{1}{3}=0\)
\(x=0-\frac{1}{3}\)
\(x=-\frac{1}{3}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=-\frac{1}{3}\end{cases}}\)