Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,x\in\left\{15;20;...;70;75\right\}\\ b,x\in\left\{6;8;12\right\}\)
\(x\) \(⋮\) \(5\) và \(13 < x \) \(\le\) \(78\)
\(x = \) \(\left\{15;20;25;30;35;40;45;50;55;60;65;70;75\right\}\)
\(12\) \(⋮\) \(x\) và \(x > 4\)
\(x = \) \(\left\{6;12\right\}\)

a) \(243^5=\left(3^5\right)^5=3^{25}\)
\(3\cdot27^5=3\cdot\left(3^3\right)^5=3\cdot3^{15}=3^{16}\)
mà \(3^{25}>3^{16}\)
nên \(243^5>3\cdot27^5\)
b) \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
mà \(5^{20}< 5^{21}\)
nên \(625^5< 125^7\)
c) \(202^{303}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=\left(303^2\right)^{101}=91809^{101}\)
mà \(8242408^{101}>91809^{101}\)
nên \(202^{303}>303^{202}\)

a: \(17A=\dfrac{17^{19}+17}{17^{19}+1}=1+\dfrac{16}{17^{19}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}=1+\dfrac{16}{17^{18}+1}\)
mà 17^19+1>17^18+1
nên A<B
b: \(2C=\dfrac{2^{2021}-2}{2^{2021}-1}=1-\dfrac{1}{2^{2021}-1}\)
\(2D=\dfrac{2^{2022}-2}{2^{2022}-1}=1-\dfrac{1}{2^{2022}-1}\)
2^2021-1<2^2022-1
=>1/2^2021-1>1/2^2022-1
=>-1/2^2021-1<-1/2^2022-1
=>C<D

\(1,\\ 16^x< 128^4\Rightarrow\left(2^4\right)^x< \left(2^6\right)^4\Rightarrow2^{4x}< 2^{24}\\ \Rightarrow4x=24\Rightarrow x=6\\ 2,\\ 3^{99}=\left(3^3\right)^{33}=27^{33}>27^{21}>11^{21}\)

a: Ta có: \(3^{2x+1}< 27\)
\(\Leftrightarrow2x+1< 3\)
\(\Leftrightarrow x< 1\)
hay x=0

a: 99^20=9801^10<9999^10
b: 3^500=243^100
5^300=125^300
=>3^500>5^300

Giải:
a) Gọi dãy đó là A, ta có:
\(A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2014}}\)
\(2A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2013}}\)
\(2A-A=\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2013}}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2014}}\right)\)
\(A=\dfrac{1}{2}-\dfrac{1}{2^{2014}}\)
Vì \(\dfrac{1}{2}< 1;\dfrac{1}{2^{2014}}< 1\) nên \(\dfrac{1}{2}-\dfrac{1}{2^{2014}}< 1\)
\(\Rightarrow A< 1\)
b) \(A=\dfrac{10^{11}-1}{10^{12}-1}\) và \(B=\dfrac{10^{10}+1}{10^{11}+1}\)
Ta có:
\(A=\dfrac{10^{11}-1}{10^{12}-1}\)
\(10A=\dfrac{10^{12}-10}{10^{12}-1}\)
\(10A=\dfrac{10^{12}-1+9}{10^{12}-1}\)
\(10A=1+\dfrac{9}{10^{12}-1}\)
Tương tự:
\(B=\dfrac{10^{10}+1}{10^{11}+1}\)
\(10B=\dfrac{10^{11}+10}{10^{11}+1}\)
\(10B=\dfrac{10^{11}+1+9}{10^{11}+1}\)
\(10B=1+\dfrac{9}{10^{11}+1}\)
Vì \(\dfrac{9}{10^{12}-1}< \dfrac{9}{10^{11}+1}\) nên \(10A< 10B\)
\(\Rightarrow A< B\)
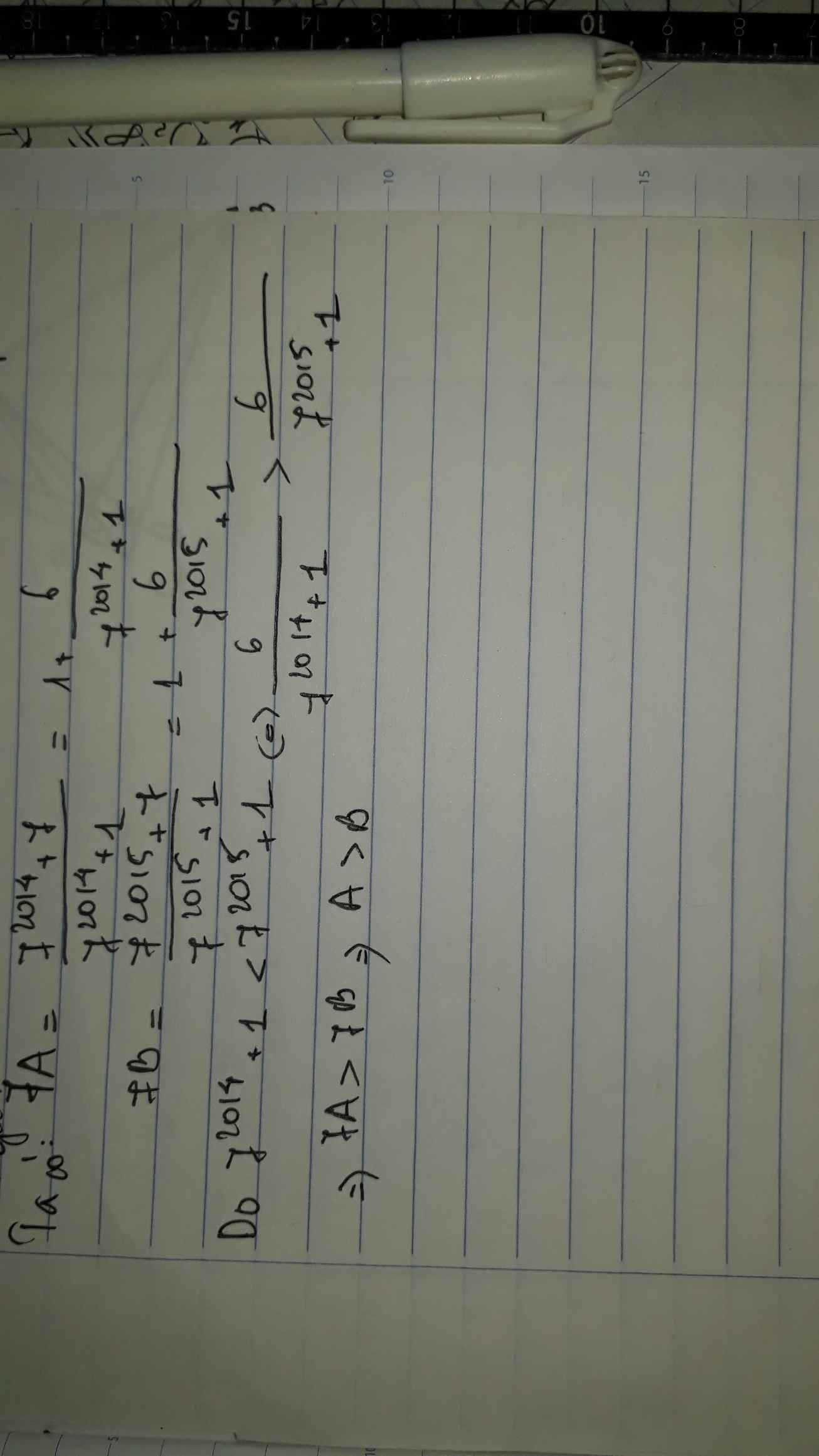
a) 2435 = (35)5 = 325
3.278 = 3.(33)8 = 3.324 = 325
Vì 325 = 325 => 2435 = 3.278.
b) 1512 = 312.512
813.1255 = (34)3.(53)5 = 312.515
Ta có 312 = 312 và 512 < 515 => 1512 < 813.1255
c) Ta có: 7811 > 7810 => 7812 - 7811 < 7812 - 7810
a) 2435 và 3.278
Ta có : 2435 = (27 . 9)5 = 275 . 95 = (33)5 . (32)5 = 315 . 310 = 325
3.278 = 3.(33)8 = 3.324 = 325
Mà : 25 = 25 => 325 = 325 hay 2435 = 3.278
b) 1512 và 813 . 1255
Ta có : 1512 = 312 . 512
813 = 312 ; 1255 = 515
Mà : 12 = 12 => 312 = 312 ; 15>12 => 515 > 512
=> 312 .512 < 312 . 515 hay 1512 < 813 . 1255
c) 7812 - 7811 và 7812 - 7810
Ta có : 7812 - 7811 = 7810( 782 - 78 ) = 7810 . 6006
7812 - 7810 = 7810(782 - 1 ) = 7810 . 6083
Mà 6006 < 6083 => 7812 - 7811 < 7812 - 7810
C2 : Vì 11> 10 => 78^11 > 78^10 => 78^12 - 78^11 < 78^12 - 78^10