Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Chứng minh được tam giác ABH= tam giác ACH( ch-cgv)
Suy ra: HB=HC(yttư)(đpcm). Vậy H là trung điểm BC.Suy ra HB=HC=BC:2=8:2=4
và góc BAH=góc CAH(yttư)(đpcm)
b) Ta có: tam giác ABH vuông tại H(AH vuông góc BC)
Suy ra AH^2 + BH^2 =AB^2
Suy ra AH^2+4^2= 5^2
Suy ra AH^2= 9
Mà AH>0
Suy ra AH=3
c) Xét tam giác ADH và tam giác AEH, ta có:
Góc ADH= Góc AEH=90 ĐỘ ( HD vuông góc AB, HE vuông góc AC)
AH là cạnh chung
Góc DAH= Góc EAH(yttư do tam giác ABH= tam giác ACH)
Suy ra tam giác ADH= tam giác AEH(ch-gh)
Suy ra HD=HE(yttư)
Suy ra tam giác HDE cân tại H(đpcm)

tu ve hinh :
AB = AC => tamgiac ABC can tai A (dn)
xet tamgiac AHB va tamgiac AHC co :
AB = AC va goc ABC = gocACB do tamgiac ABC can tai A (cmt)
goc AHB = goc AHC = 90 do AH | BC (gt)
=> tamgiac AHB = tamgiac AHC (ch - gn)
=> HB = HC (dn)
b, cau nay de tu ap dung PY-TA-GO ma lam
c,
+ xet tamgiac DHB va tamgiac EHC co :
goc ABC = goc ACB (cau a)
BH = HC (cau a)
goc BDH = goc HEC = 90 do HD | AB va HE | AC (gt)
=> tamgiac DHB = tamgiac EHC(ch - gn)
=> DH = DE (dn)
=> tamgiac DHE can tai H (dn)
+ co AD + DB = AB
AE + EC = AC
AB = AC (cau a)
BD = EC do tamgiac HDB = tamgiac HEC (cau b)
=> DA = AE
DE cat AH tai O
xet tamgiac DAO va tamgiac EAO co : AO chung
goc BAH = goc CAH do tamgiac AHB = tamgiac AHC (cau a)
=> tamgiac DAO = tamgiac EAO (c - g - c)
=> AD = AE (dn)
=> tamgiac ADE can tai A (dn)
=> goc ADE = (180 - goc BAC) : 2 (tc)
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc ADE = goc ABC ma 2 goc nay dong vi
=> DE//BC (tc)
- tự vẽ hình
a)Xét 2 tam giác vuông ABH và ACH, ta có:
AB=AC(tam giác ABC cân tại A)
Góc ABH = góc ACH(tam giác ABC cân tại A)
Vậy tam giác vuông ABH = tam giác vuông ACH
=> HB=HC(cặp cạnh t/ứng)
và góc BAH = góc CAH (cặp góc t/ứng)
b) Ta có HB=HC(cmt)
mà HB+HC=8 (cm) => HB=HC=4(cm)
Áp dụng định lý pytago vào tam giác vuông AHB, ta có:
AH2+BH2=AB2
=> AH2=AB2-BH2=25-16=9 => AH=3
c) Xét tam giác vuông BDH và tam giác vuông CEH, ta có:
BH=HC(cmt)
góc DBH=góc ECH(tam giác ABC cân tại A)
Vậy tam giác vuông BDH = tam giác vuông CEH
=> DH=EH(cặp cạnh t/ứng)
=> tam giác HDE là tam giác cân tại H
d) c/m DE//BC( ko có câu d nhưng vt cho dễ nhìn)
Góc BHD=Góc CHE(tam giác vuông BDH = tam giác vuông CEH)
Ta có: Góc BHD + góc CHE+ góc DHE=180 độ
-Góc HDE+Góc DEH+ Góc DHE-180 độ(tổng 3 góc của 1 tam giác)
Mà Góc BHD=Góc CHE và Góc HDE=Góc DEH(tam giác HDE cân tại H)
=> Góc BHD=Góc CHE = Góc HDE=Góc DEH
Mà hai góc DEH và CHE ở vị trí so le trong
=> DE//BC

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H

tự vẽ hình nha :
xét tam giác ABH và tam giác ACH có:
AB=AC
góc ABH= góc ACH
góc AHB= góc AHC
=>tam giác abh = tam giác ach(ch-gn)
=>hb=hc=>bah=Cah
có hb=hc =bc/2=8/2=4
xét tam giác abh
ab^2=bh^2+Ah^2
=>ah^2=9=>ah=3
c)xét tam giác bdh vg tai d
tam giác ceh vg tại e
bh=hc cm trên
góc b=góc c
=> tam giác dbh =tam giác ech
=>db=ec
=>ad=ae=.. tam giác ade cân
tam giác abc cân tại a
tam giác ade cân tại a góc a chung =>góc ade= góc aed=góc b =bóc c
vì aed=góc c=>de//bc đồng vị

a) Chứng minh được tam giác ABH= tam giác ACH (ch-cgv)
Suy ra: HB=HC (2 góc tương ứng). Vậy H là trung điểm BC.
Suy ra HB=HC=BC:2=8:2=4
và góc BAH=góc CAH.
b) Ta có: tam giác ABH vuông tại H(AH vuông góc BC)
Suy ra AH^2 + BH^2 =AB^2
Suy ra AH^2+4^2= 5^2
Suy ra AH^2= 9
Mà AH>0
Suy ra AH=3
c) Xét tam giác ADH và tam giác AEH có:
+ Góc ADH = Góc AEH = 90o (HD vuông góc AB, HE vuông góc AC)
+ AH là cạnh chung
+ Góc DAH= Góc EAH(do tam giác ABH= tam giác ACH)
=> tam giác ADH = tam giác AEH (ch-gh)
Suy ra HD=HE (2 góc tương ứng)
Suy ra tam giác HDE cân tại H.
Xét ΔAHBvà ΔAHCΔAHBvàΔAHCcó:
AHBˆ=AHC=ˆAHB^=AHC=^90 độ ( gt )
AH là cạnh chung
AB=AC=5cm ( gt )
Do đó: ΔABH=ΔACHΔABH=ΔACH( cạnh huyền-cạnh góc vuông)
⇒HB=HC⇒HB=HC( 2 cạnh tương ứng )
b) Ta có: HB = HC = 12.BC=12.8=82=412.BC=12.8=82=4 cm
Áp dụng định lí Py-ta-go vào ΔAHBΔAHB vuông tại H, ta có:
BA2=BH2+AH2BA2=BH2+AH2
hay: 52=42+AH2⇒AH2=52−42=52=42+AH2⇒AH2=52−42= 25 - 16 = 9 = 3232
Vậy AH = 3 cm.
c) Xét ΔHDBvà ΔHECΔHDBvàΔHEC, ta có:
HDBˆ=HECˆHDB^=HEC^ = 90 độ ( gt )
BH = CH ( câu a )
Do đó: ΔHDB=ΔHECΔHDB=ΔHEC( cạnh huyền - góc nhọn )
⇒DH=HE⇒DH=HE ( 2 cạnh tương ứng ) (1)
Từ (1) => ΔHDEΔHDE cân tại H.
Chúc bạn học tốt ( tớ có 2 cách làm nhưng bạn kẻ hình nhé )

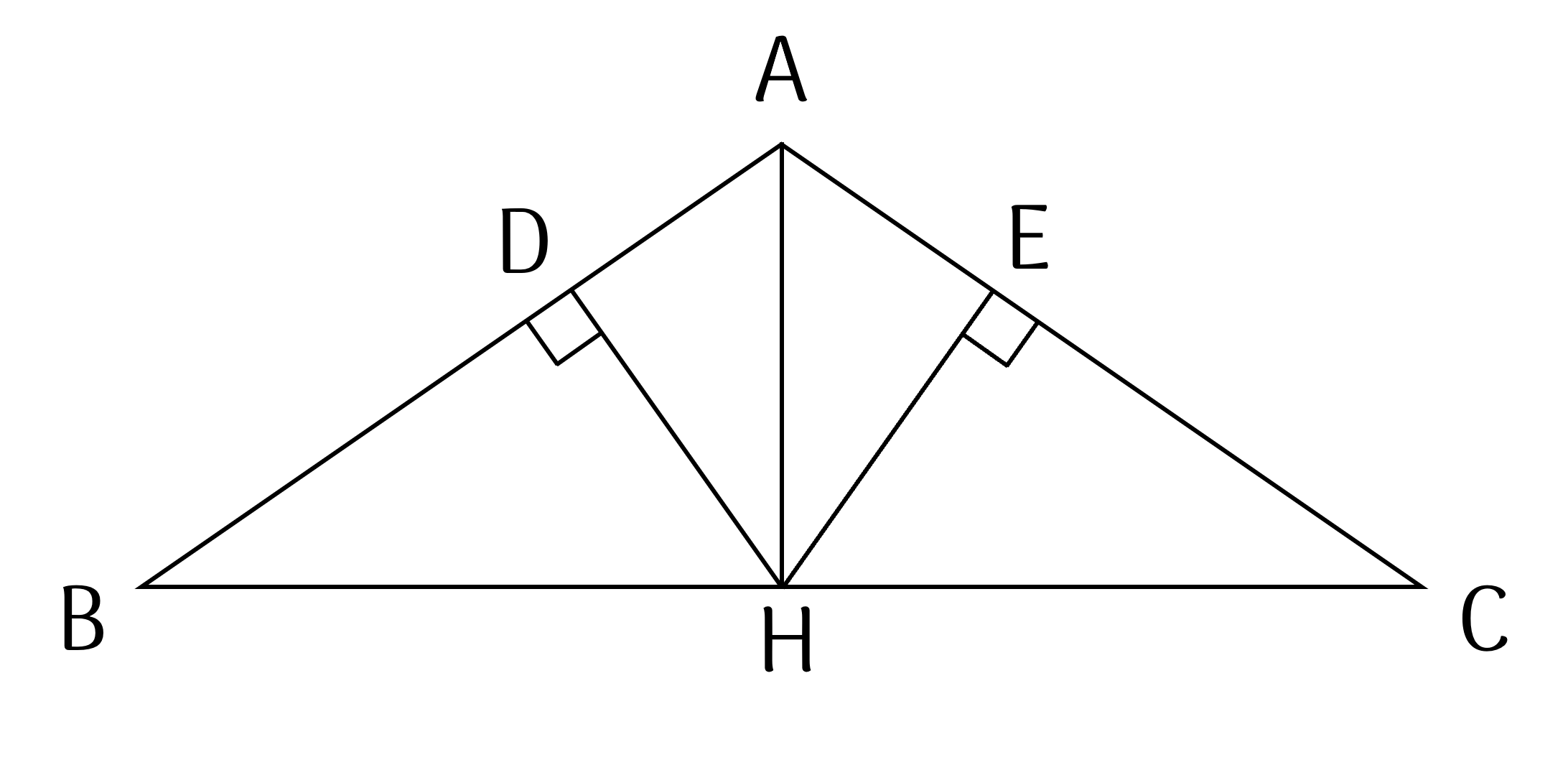
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.