Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x-1\right)^2=\left(x-1\right)^4\)
\(\Rightarrow\left(x-1\right)^2-\left(x-1\right)^4=0\)
\(\Rightarrow\left(x-1\right)^2.1-\left(x-1\right)^2.\left(x-1\right)^2=0\)
\(\Rightarrow\left(x-1\right)^2.\left[\left(x-1\right)^2-1\right]=0\)
\(\Rightarrow\orbr{\begin{cases}\left(x-1\right)^2=0\\\left(x-1\right)^2-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\\left(x-1-1\right)\left(x-1+1\right)=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=1\\x=2;x=0\end{cases}}}\)
Vậy: \(x\in\left\{1;2;0\right\}\)

Câu 1 : Ảnh của một vật tạo bởi gương cầu lồi giống ảnh của một vật tạo bởi gương phẳng ở tính chất đều là ảnh ảo; khác ở tính chất, ảnh tạo bởi gương cầu lồi nhỏ hơn ảnh tạo bởi gương phẳng.
Câu 2 : Khi một vật ở gần sát gương cầu lõm thì ảnh của vật là ảnh ảo và ảnh lớn hơn vật.

a) Xét \(\Delta BAD\) và \(\Delta BCE:\)
\(\widehat{B}chung.\)
\(\widehat{D}=\widehat{E}\left(=90^o\right).\)
\(\Rightarrow\Delta BAD\sim\Delta BCE\left(g-g\right).\)
b) Xét \(\Delta ABC:\)
CE là đường cao \(\left(CE\perp AB\right).\)
AD là đường cao \(\left(AD\perp BC\right).\)
Mà F là giao điểm của CE và AD.
\(\Rightarrow BF\) là đường cao.
Xét \(\Delta ABC\) cân tại B:
BF là đường cao (gt).
\(\Rightarrow BF\) là phân giác \(\widehat{ABC}.\)

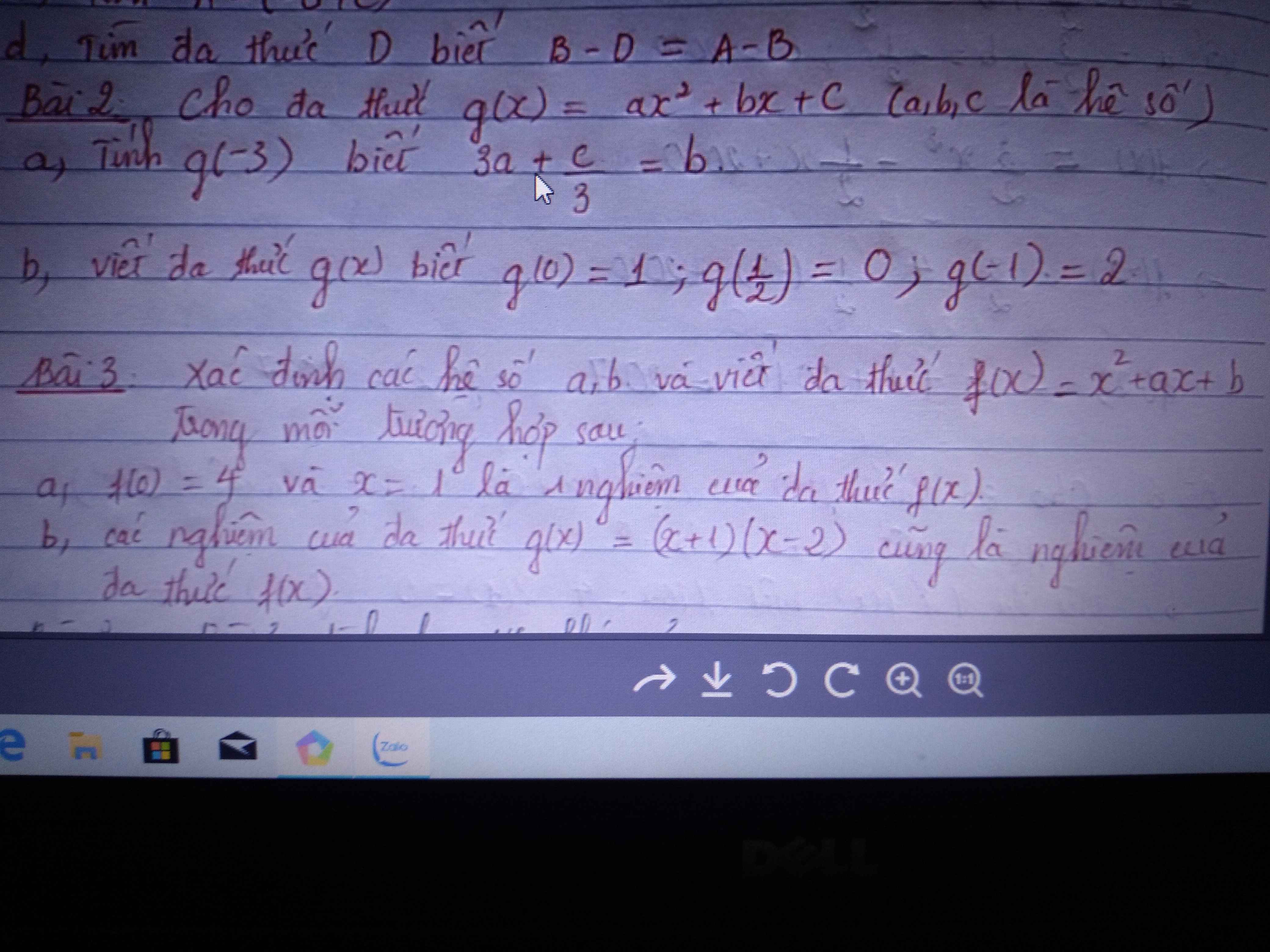
Bài 3:
a: Ta có: f(0)=4 và f(1)=0
\(\Leftrightarrow\left\{{}\begin{matrix}0^2-a\cdot0+b=4\\1^2+a\cdot1+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b+a=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=4\\a=-1-b=-5\end{matrix}\right.\)
b: Ta có: \(f\left(-1\right)=0\) và f(2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-1\right)^2-a\cdot\left(-1\right)+b=0\\2^2-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-1\\-2a+b=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a=3\\a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-1-a=-2\end{matrix}\right.\)

\(Pytago:\)
\(AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16\left(cm\right)\)
=> C
Chọn C nhé bạn