Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đây là 1 lời giải sai em
Đơn giản vì phương trình gốc không thể giải được

TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`
Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`
`=>` Không nằm trong TXĐ.

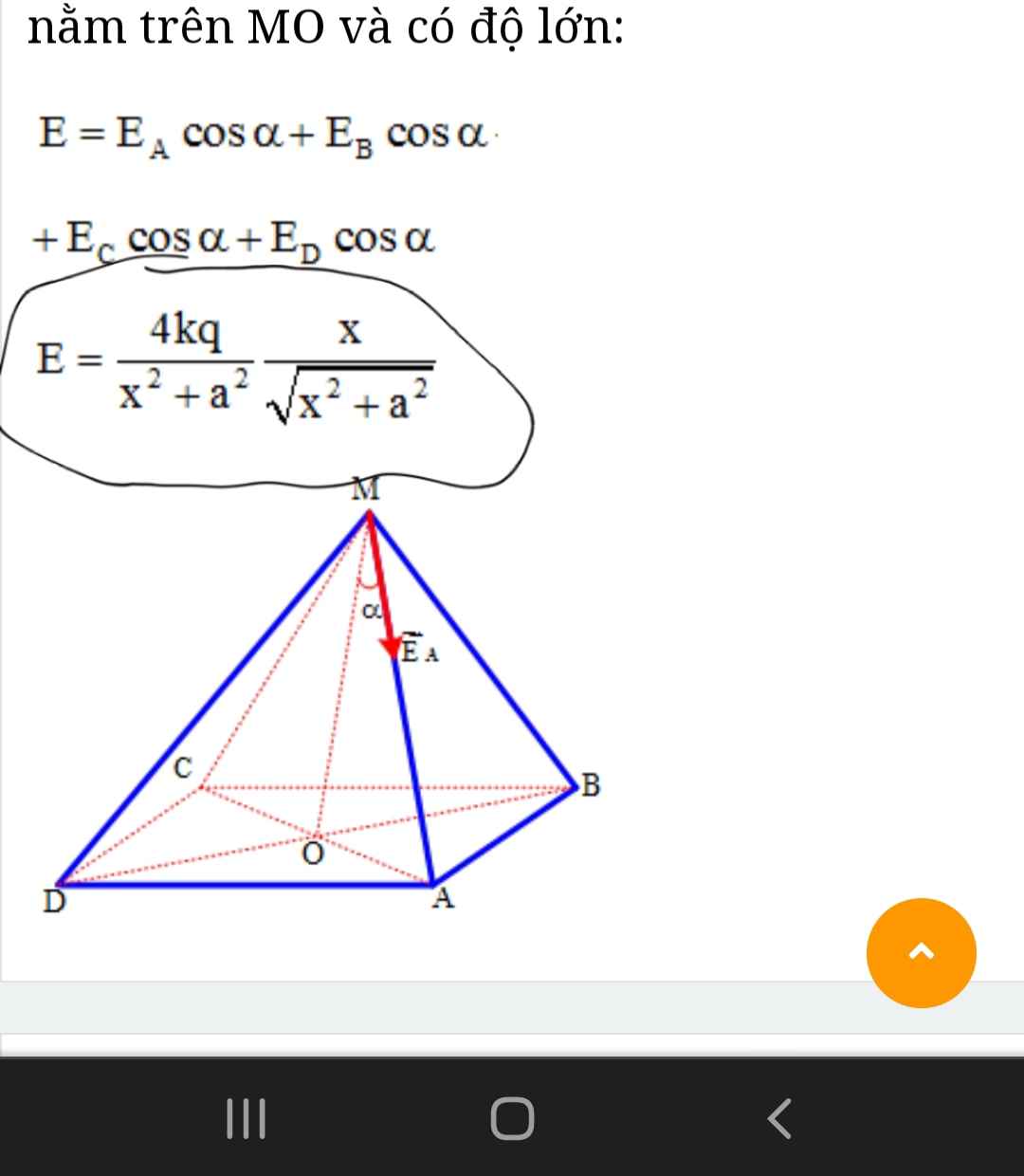
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)

1/
Bạn chỉ cần tìm sin, cos trong \(\left[0;2\pi\right]\) là đủ (vì cả 2 hàm đều tuần hoàn với chu kì \(2\pi\))
Đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\) với \(a\in\left[0;2\pi\right]\)
\(\Rightarrow4sina.cosa\left(2cos^2a-1\right)=1\)
\(\Leftrightarrow2sin2a.cos2a=1\Leftrightarrow sin4a=1\)
\(\Rightarrow4a=\frac{\pi}{2}+k2\pi\Rightarrow a=\frac{\pi}{8}+\frac{k\pi}{2}\)
\(\Rightarrow0\le\frac{\pi}{8}+\frac{k\pi}{2}\le2\pi\Rightarrow a=\left\{\frac{\pi}{8};\frac{5\pi}{8};\frac{9\pi}{8};\frac{13\pi}{8};\frac{17\pi}{8}\right\}\)
\(\Rightarrow\left(x;y\right)=\left(sin\frac{\pi}{8};cos\frac{\pi}{8}\right);\left(sin\frac{5\pi}{8};cos\frac{5\pi}{8}\right)...\)
2.
\(sinx=\frac{1}{3}\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{3}\right)+l2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)\\x=\pi-arcsin\left(\frac{1}{3}\right)\end{matrix}\right.\)
(Vì \(0< \frac{1}{3}< 1\) nên \(0< arcsin\left(\frac{1}{3}\right)< \frac{\pi}{2}\) do đó nếu \(k>0\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi>2\pi\) ; nếu \(k\le-1\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi\le-\frac{3\pi}{2}\) đều ko thuộc \(\left[0;\pi\right]\Rightarrow k=0\).
Tương tự với \(l\))
Cho mình hỏi sao từ 0 < 1/3 < 1 thì suy ra đc 0 < arcsin (1/3) < pi/2 vậy?

Sử dụng công thức: \(cos\alpha=sin\left(90^0-\alpha\right)\)


Cách 1 chắc chắn sai vì pt d' ko cùng phương với d
Còn sai ở đâu thì nhìn cách làm rối loạn quá nên ko biết
Làm cách 1 theo kiểu "cơ bản" thì:
\(A\left(-1;1\right)\Rightarrow\left\{{}\begin{matrix}x_{A'}=-3.\left(-1\right)+\left(1-\left(-3\right)\right).\left(-1\right)=-1\\y_{A'}=-3.1+\left(1-\left(-3\right)\right).3=9\end{matrix}\right.\) \(\Rightarrow A'\left(-1;9\right)\)
\(B\left(2;-1\right)\Rightarrow\left\{{}\begin{matrix}x_{B'}=-3.2+\left(1-\left(-3\right)\right).\left(-1\right)=-10\\y_{B'}=-3.\left(-1\right)+\left(1-\left(-3\right)\right).3=15\end{matrix}\right.\) \(\Rightarrow B'\left(-10;15\right)\)
\(\Rightarrow\overrightarrow{A'B'}=\left(-9;6\right)=3\left(-3;2\right)\)
Phương trình A'B':
\(2\left(x+1\right)+3\left(y-9\right)=0\Leftrightarrow2x+3y-25=0\)