Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các đỉnh, cạnh, mặt của một đa diện phải thoả mãn những tính chất:
- Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một đỉnh chung.
- Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Phương pháp:
- Dựng thiết diện cắt bởi (AB 'M) với hình hộp.
- Sử dụng phương pháp cộng trừ thể tích khối đa diện suy ra các tỉ số thể tích.
Cách giải:
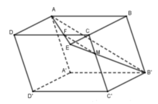
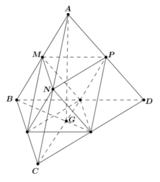
Dựng thiết diện cắt bởi (AB 'M) với hình hộp như hình vẽ.
Ta có: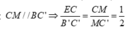 
Đặt thể tích 
Mà 
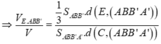
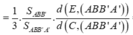
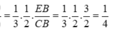
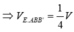
Lại có
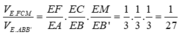
Đáp án A
Chọn C.
Dựa vào định nghĩa khối đa diện. Mỗi cạnh là cạnh chung của đúng hai mặt.
Đáp án C
Xét hình đa diện là hình tứ diện thì kết quả về quan hệ số đinh và số mặt thỏa mãn đáp án C
Cho khối đa diện G có các đỉnh là 
lần lượt là số các mặt của H nhận chúng làm đỉnh chung. Tổng số các cạnh của G là:
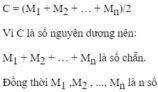
tự nhiên lẻ nên tổng của chúng là số chẵn khi n chẵn.
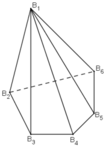
Ví dụ: Hình chóp ngũ giác 
là đỉnh chung của 5 mặt bên. Mỗi đỉnh
B 1 , B 2 , B 3 , B 4 , B 5 , B 6 là đỉnh chung của ba mặt (hình trên).
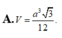
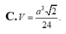
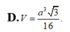
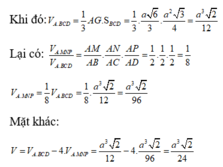
Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất:
- Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh, ba mặt;
- Mỗi cạnh là cạnh chung của đúng hai mặt;
- Hai mặt bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có đúng một cạnh chung.