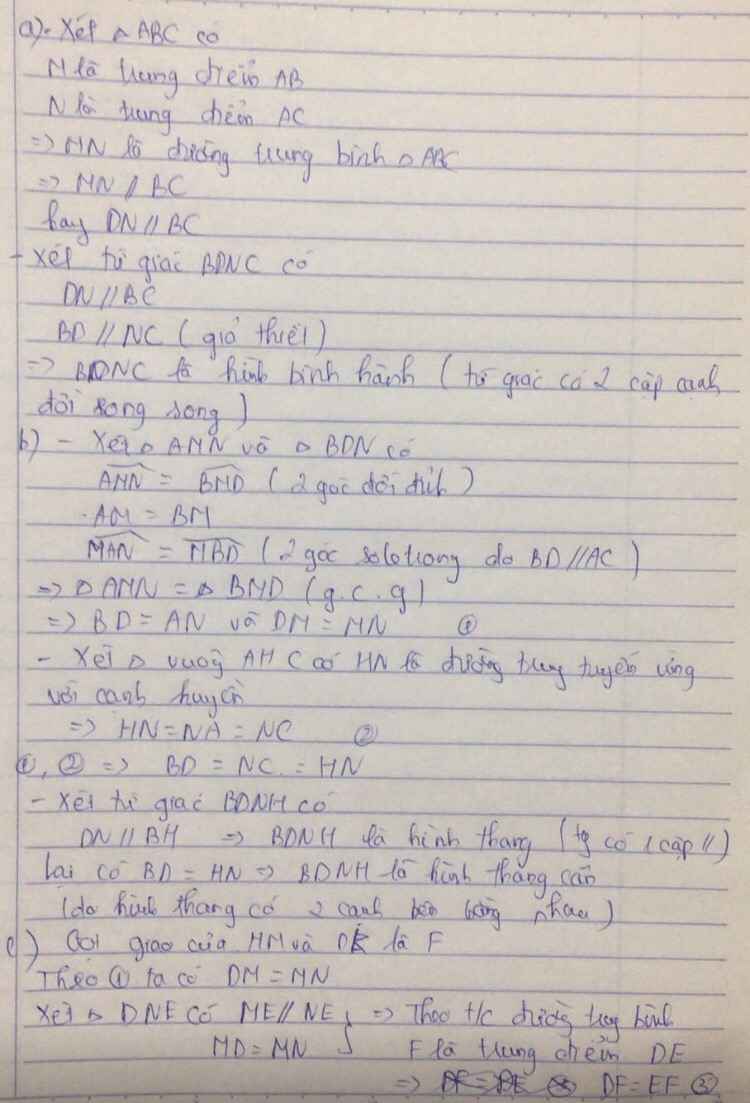Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

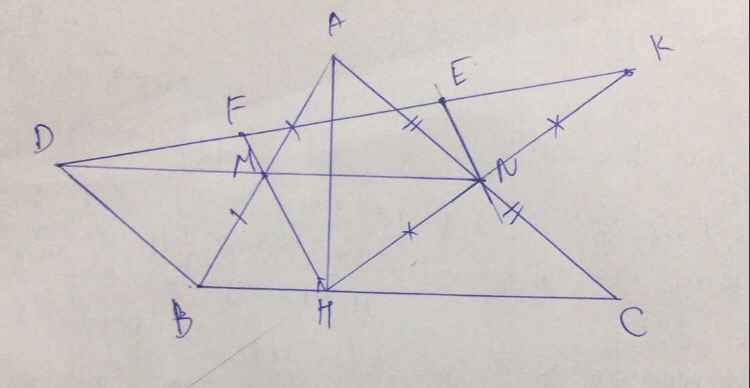
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
Xét tứ giác BDNC có
DN//BC
BD//NC
Do đó: BDNC là hình bình hành
b: Xét tứ giác BDNH có BH//DN
nên BDNH là hình thang

Hướng dẫn a,b
Tự vẽ hình
a) M , N là trung điểm AB , AC => MN là đường trung bình của tam giác ABC
=> MN//BC => DN//BC . Mà BD// NC => Tứ giác BDNC là hbh
b) Có \(\widehat{NCH}=\widehat{NDB}\) ( hình bình hành )
Tam giác AHC vuông có trung tuyến HN = 1/2 AC = NC => Tam giác NHC cân => \(\widehat{NCH}=\widehat{NHC}\)
=> \(\widehat{NDB}=\widehat{NHC}\)
Mà NHC = NHD (so le trong ) = > NHD = NBD
=> BDNH là hình thang cân

a: Xét tứ giác AKMN có
MN//AK
AN//MK
Do đó: AKMN là hình bình hành
mà \(\widehat{NAK}=90^0\)
nên AKMN là hình chữ nhật
b: Xét ΔAMQ có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAMQ cân tại A
mà AN là đường cao
nên AN là tia phân giác của góc MAQ(1)
Xét ΔAME có
AK là đường cao
AK là đường trung tuyến
DO đó: ΔAME cân tại A
mà AK là đường cao
nên AK là tia phân giác của góc MAE(2)
Từ (1) và (2) suy ra \(\widehat{QAE}=2\cdot\left(\widehat{MAN}+\widehat{MAK}\right)=2\cdot90^0=180^0\)
hay Q,E,A thẳng hàng