Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=> A = ( 1 + 2 + 22 + 23 + 24 ) + ( 25 + 26 + 27 + 28 + 29 ) + .... + ( 296 + 297 + 298 + 299 + 2100 )
=> A = 31 + 25 . ( 1 + 2 + 22 + 23 + 24 ) + .... + 296.( 1 + 2 + 22 + 23 + 24 )
=> A = 31 + 25 . 31 + .... + 296 . 31
=> A = 31 . ( 1 + 25 + 210 + .... + 296 )
Vì 31 chia hết cho 31 nên A chia cho 31 dư 0
\(A=1+\left(2+2^2+2^3+2^4+2^5\right)+....+\left(2^{96}+2^{97}+2^{98}+2^{99}+2^{100}\right)\)
\(A=1+2.31+....+2^{96}.31=31.\left(2+2^6+...+2^{96}\right)+1\)
Chia 31 dư 1

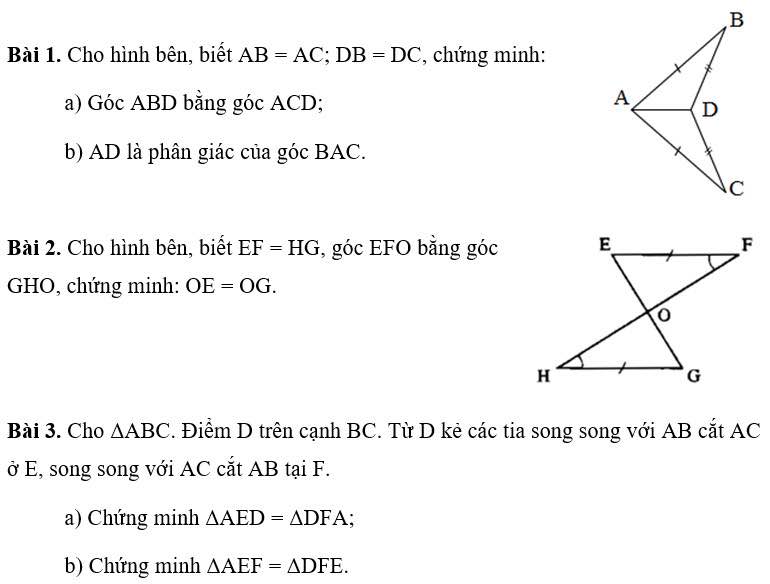
Bài 1 :
a,Có \(AD\) chung , mà \(AB=AC;DB=DC\)
\(\Rightarrow\Delta ABC=\Delta ADC\)
Do đó \(\widehat{ABD}=\widehat{ACD}\)
b,\(AD\) là cạnh chung của 2\(\Delta:\Delta ABD,\Delta ACD\)
\(\Rightarrow AD\) là phân giác của \(\widehat{BAC}\)
Bài 2:
Ta có : \(EF=HG,\widehat{EFO}=\widehat{GHO}\)
Theo TH thứ 2 của 2 tam giác bằng nhau ta có : cạnh - góc - cạnh
\(\Rightarrow OE=OG\)
Bài 3: Có hình ko bn ,mk dựa vào hình lm ko mk lười vẽ hình lắm =(((((((

A=1+3/2^3+4/2^4+5/2^5+...100/2^100
1/2*A = 1/2 + 3/2^4 + 4/2^5 +....+ 99/2^100 + 100/2^101
A- A/2 = 1/2A =1/2 + 3/2^3 + 1/2^4 +...+1/2^100 - 100/2^101
= [1/2+1/2^2 +1/2^3 +...+1/2^100] -100/2^101 (Do 3/2^3 = 1/2^2 +1/2^3)
=[1-(1/2)^101]/(1-1/2) -100/2^101
=(2^101 -1)/2^100 - 100/2^101
=> A = (2^101 -1)/2^99 - 100/2^100
Bạn ơi khó hiểu quá bạn giải chi tiết hơn giúp mình nhé mình sẽ k cho bạn 2 cái nhé

Đặt A=1+2+22+..............+22017
\(\Rightarrow\)2A =2+22+23+.............+22018
\(\Rightarrow\)2A -A = (2+22+23+............+22018) -(1+2+22 +...............+22017)
\(\Rightarrow\)A= 22018 -1
Lại có :A = ( 23 )672 .22 -1 =(7+1)672 .22 -1= ( B(7) +1).22 -1 =22 .B(7) +22-1=22 .B(7)+3
Vây A chia 7 dư 3

 Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
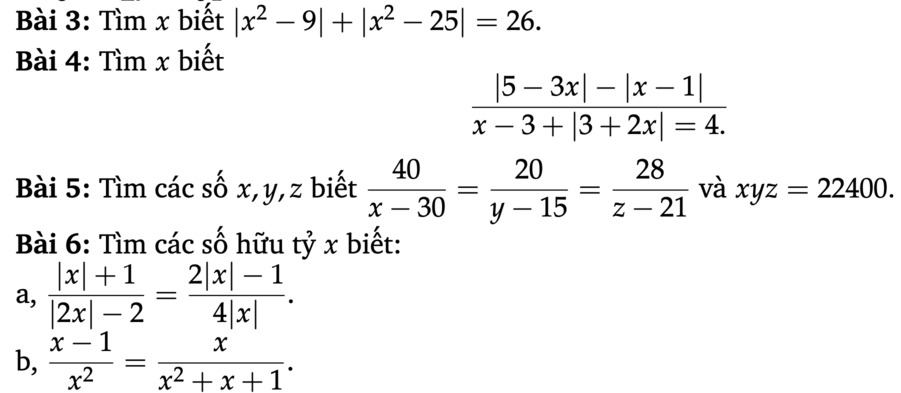 (mình sẽ tích cho tất cả các bạn)
(mình sẽ tích cho tất cả các bạn)
mình đang xin cách giải chứ kết quả biết rồi
tham khảo câu hỏi tương tự nha bạn