Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)


a, A,H,O thẳng hàng vì AH,AO cùng vuông góc với BC
HS tự chứng minh A,B,C,O cùng thuộc đường tròn đường kính OA
b, Ta có K D C ^ = A O D ^ (cùng phụ với góc O B C ^ )
=> ∆KDC:∆COA (g.g) => AC.CD = CK.AO
c, Ta có: M B A ^ = 90 0 - O B M ^ và M B C ^ = 90 0 - O M B ^
Mà O M B ^ = O B M ^ (∆OBM cân) => M B A ^ = M B C ^
=> MB là phân giác A B C ^ . Mặt khác AM là phân giác B A C ^
Từ đó suy ra M là tâm đường tròn nội tiếp tam giác ABC
d, Kẻ CD ∩ AC = P. Chứng minh ∆ACP cân tại A
=> CA = AB = AP => A là trung điểm CK

Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450
Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450vv

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

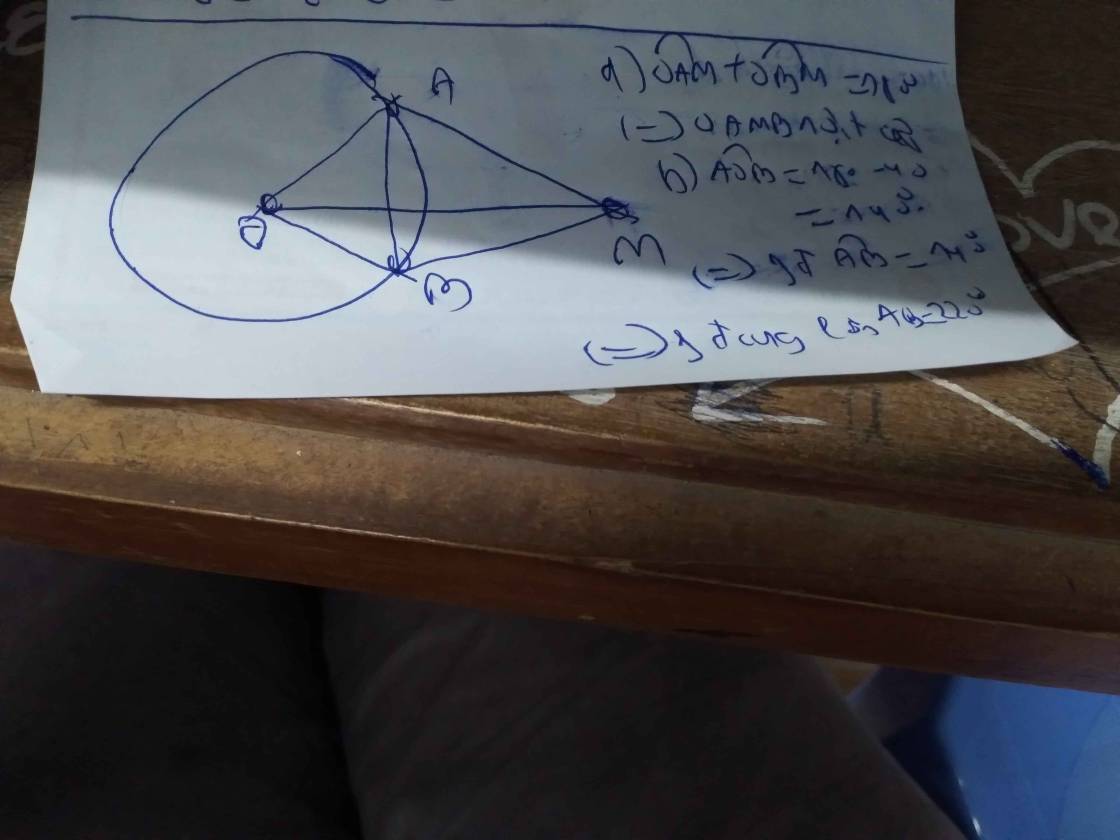
2:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
góc OKM=góc OAM=góc OBM=90 độ
=>O,P,A,M,B cùng nằm trên đường tròn đường kính OM
góc AKM=góc AOM
góc BKM=góc BOM
mà góc AOM=góc BOM
nên góc AKM=góc BKM
=>KM là phân giác của góc AKB