Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ ĐKXĐ: \(x>\frac{1}{2}\)
\(\Leftrightarrow\frac{3x^2-1}{\sqrt{2x-1}}-\sqrt{2x-1}=mx\)
\(\Leftrightarrow\frac{3x^2-2x}{\sqrt{2x-1}}=mx\Leftrightarrow\frac{3x-2}{\sqrt{2x-1}}=m\)
Đặt \(\sqrt{2x-1}=a>0\Rightarrow x=\frac{a^2+1}{2}\Rightarrow\frac{3a^2-1}{2a}=m\)
Xét hàm \(f\left(a\right)=\frac{3a^2-1}{2a}\) với \(a>0\)
\(f'\left(a\right)=\frac{12a^2-2\left(3a^2-1\right)}{4a^2}=\frac{6a^2+2}{4a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến
Mặt khác \(\lim\limits_{a\rightarrow0^+}\frac{3a^2-1}{2a}=-\infty\); \(\lim\limits_{a\rightarrow+\infty}\frac{3a^2-1}{2a}=+\infty\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
b/ ĐKXĐ: \(x\ge2\)
\(\Leftrightarrow\sqrt[4]{\left(x-1\right)^2}+4m\sqrt[4]{\left(x-1\right)\left(x-2\right)}+\left(m+3\right)\sqrt[4]{\left(x-2\right)^2}=0\)
Nhận thấy \(x=2\) không phải là nghiệm, chia 2 vế cho \(\sqrt[4]{\left(x-2\right)^2}\) ta được:
\(\sqrt[4]{\left(\frac{x-1}{x-2}\right)^2}+4m\sqrt[4]{\frac{x-1}{x-2}}+m+3=0\)
Đặt \(\sqrt[4]{\frac{x-1}{x-2}}=a\) pt trở thành: \(a^2+4m.a+m+3=0\) (1)
Xét \(f\left(x\right)=\frac{x-1}{x-2}\) khi \(x>0\)
\(f'\left(x\right)=\frac{-1}{\left(x-2\right)^2}< 0\Rightarrow f\left(x\right)\) nghịch biến
\(\lim\limits_{x\rightarrow2^+}\frac{x-1}{x-2}=+\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\frac{x-1}{x-2}=1\) \(\Rightarrow f\left(x\right)>1\Rightarrow a>1\)
\(\left(1\right)\Leftrightarrow m\left(4a+1\right)=-a^2-3\Leftrightarrow m=\frac{-a^2-3}{4a+1}\)
Xét \(f\left(a\right)=\frac{-a^2-3}{4a+1}\) với \(a>1\)
\(f'\left(a\right)=\frac{-2a\left(4a+1\right)-4\left(-a^2-3\right)}{\left(4a+1\right)^2}=\frac{-4a^2-2a+12}{\left(4a+1\right)^2}=0\Rightarrow a=\frac{3}{2}\)
\(f\left(1\right)=-\frac{4}{5};f\left(\frac{3}{2}\right)=-\frac{3}{4};\) \(\lim\limits_{a\rightarrow+\infty}\frac{-a^2-3}{4a+1}=-\infty\)
\(\Rightarrow f\left(a\right)\le-\frac{3}{4}\Rightarrow m\le-\frac{3}{4}\)

Bất phương trình x2-3x+2 ≤ 0 ⇔ 1 ≤ x ≤ 2
Bất phương trình mx2+(m+1) x+m+1 ≥ 0
![]()
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 , 1 ≤ x ≤ 2
Có f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.

Giải bất phương trình x2- 3x+ 2≤ 0 ta được 1≤x≤2.
Bất phương trình mx2+ (m+ 1) x+ m+1≥0
⇔ m ( x 2 + x + 1 ) ≥ - x - 2 ⇔ m ≥ - x - 2 x 2 + x + 1
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 với 1≤ x≤ 2
Có đạo hàm f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 , ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.

Hướng dẫn:
Bạn khảo sát hàm \(y=f\left(x\right)=2x^3-9x^2+12x\) với \(x\ge0\)
Sau đó lấy đối xứng đồ thị (hoặc BBT) qua trục Oy sẽ được hàm \(y=f\left(\left|x\right|\right)=2\left|x\right|^3-9x^2+12\left|x\right|\)
Nhìn vào đồ thị (hoặc BBT), bạn biện luận số giao điểm của \(y=-m\) và \(y=f\left(\left|x\right|\right)\) dễ dàng


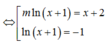

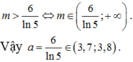


Chọn A.
ĐK: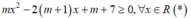
TH1: m = 0:
TH2:
Vậy BPT đã cho vô nghiệm khi m ≥ 1 5