Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi A là số tiền gốc người đó nợ.
r là lãi suất.
a là số tiền người đó trả mỗi tháng.
Sau một tháng kể từ ngày người đó mua xe, số tiền còn nợ là A 1 + r − a (triệu đồng).


Chọn C
Do lãi suất theo năm là 8% nên lãi suất tính theo tháng là
![]()
Cuối tháng 1, sau khi trả nợ 2 triệu, ông Bình còn nợ: ![]() triệu đồng.
triệu đồng.
Cuối tháng 2, sau khi trả nợ 2 triệu, ông Bình còn nợ:
![]()
![]() triệu đồng.
triệu đồng.
Cuối tháng 3, sau khi trả nợ 2 triệu, ông Bình còn nợ ![]()
![]()
….
Cuối tháng m, sau khi trả nợ 2 triệu, ông Bình còn nợ 0 đồng, nghĩa là
Ta có ![]() là tổng tất cả các số hạng của một cấp số nhân có
u
1
=
1
và công bội
q
=
n
+
1
gồm m số hạng
là tổng tất cả các số hạng của một cấp số nhân có
u
1
=
1
và công bội
q
=
n
+
1
gồm m số hạng ![]()
![]()

Ta có 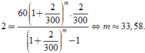
Vậy ông Bình trả hết nợ sau 34 tháng.

Đáp án D
Sau tháng 1: A 1 = 500 1 + 1 , 2 % − 10
Cuối tháng 2: A 2 = A 1 . 1 + 1 , 2 % − 10 = 500 1 + 1 , 2 % 2 − 10 1 + 1 , 2 % − 10
…..
Cuối tháng n:
A n = 500 1 + 1 , 2 % n − 10. 1 + 1 , 2 % n − 1 − ... − 10 = 500 1 + 1 , 2 % n − 10. 1 + 1 , 2 % n − 1 1 + 1 , 2 % − 1 = 0
⇒ 5 + 1 + 1 , 2 % n − 25 3 . 1 + 1 , 2 % n − 1 = 0 ⇒ 10 3 1 + 1 , 2 % n = 25 3 ⇒ n = 77

Đáp án A
Gọi T là số tiền B đã vay, r là lãi suất
Ta có:
Số tiền còn nợ sau 1 tháng là:
T 1 + r − m 1 = 1 , 01 T − 10 (với m i là số tiền mà bạn B trả tháng thứ i)
Số tiền còn nợ sau 2 tháng là:
1 , 01 T − 10 1 + r − 20 = 1 , 01 T − 10 .1 , 01 − 20 = 1 , 01 2 T − 30 , 1
Số tiền còn nợ sau 3 tháng là:
1 , 01 2 T − 30 , 1 1 + r − 30 = 1 , 01 2 T − 30 , 1 .1 , 01 − 30 = 1 , 01 3 T − 60 , 401
Cho 1 , 01 3 T − 60 , 401 = 0 ⇔ T = 58 , 62 triệu đồng.

Chọn D.
Phương pháp:
Giả sử anh A nợ ngân hàng M ngàn đồng), mỗi tháng anh A gửi vào ngân hàng a ngàn đồng, lãi suất ngân hàng là r (%). Số tiền anh A còn nợ ngân hàng :

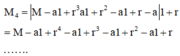

Gọi n là số tháng (tính từ năm thứ hai) mà sinh viên A trả được hết nợ, ta có:
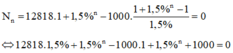
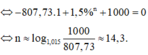
Vậy, số tháng để sinh viên A trả hết nợ là: 12 + 15 = 27 (tháng)





