Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lí Pitago
Xét tam giác ABH vuông tại H => AB2 - HB2 = AH2
Xét tam giác ACH vuông tại H => AC2 - HC2 = AH2
=> AB2 - HB2 = AC2 - HC2=AH2
=> AB2 + HC2 = AC2 + HB2

Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)

a) Ta có: \(\dfrac{HB}{HC}=\dfrac{HB.HC}{HC^2}=\dfrac{HA^2}{HC^2}=\left(\dfrac{HA}{HC}\right)^2\)
Xét \(\Delta AHC\) và \(\Delta BAC:\) Ta có: \(\left\{{}\begin{matrix}\angle AHC=\angle BAC=90\\\angle ACBchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHC\sim\Delta BAC\left(g-g\right)\Rightarrow\dfrac{HA}{HC}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2=\dfrac{c^2}{b^2}\)
b) tham khảo ở đây:https://hoc24.vn/cau-hoi/cho-dabc-vuong-tai-a-duong-cao-ah-goi-e-f-lan-luot-la-cac-hinh-chieu-cua-h-tren-ab-va-ac-cmra-aeabaf.1150118751274
a) Áp dụng hệ thức lượng trong tam giác vuông có:
\(AB^2=BH.BC\)
\(AC^2=CH.CB\)
\(\Rightarrow\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}=\dfrac{c^2}{b^2}\)
b) Áp dụng hệ thức lượng trong tam giác vuông có:
\(BH^2=BE.BA\)
\(CH^2=CF.CA\)
\(\Rightarrow\dfrac{BH^2}{CH^2}=\dfrac{BE}{CF}.\dfrac{BA}{CA}\)\(\Leftrightarrow\dfrac{c^4}{b^4}=\dfrac{BE}{CF}.\dfrac{c}{b}\)
\(\Leftrightarrow\dfrac{BE}{CF}=\dfrac{c^3}{b^3}\)
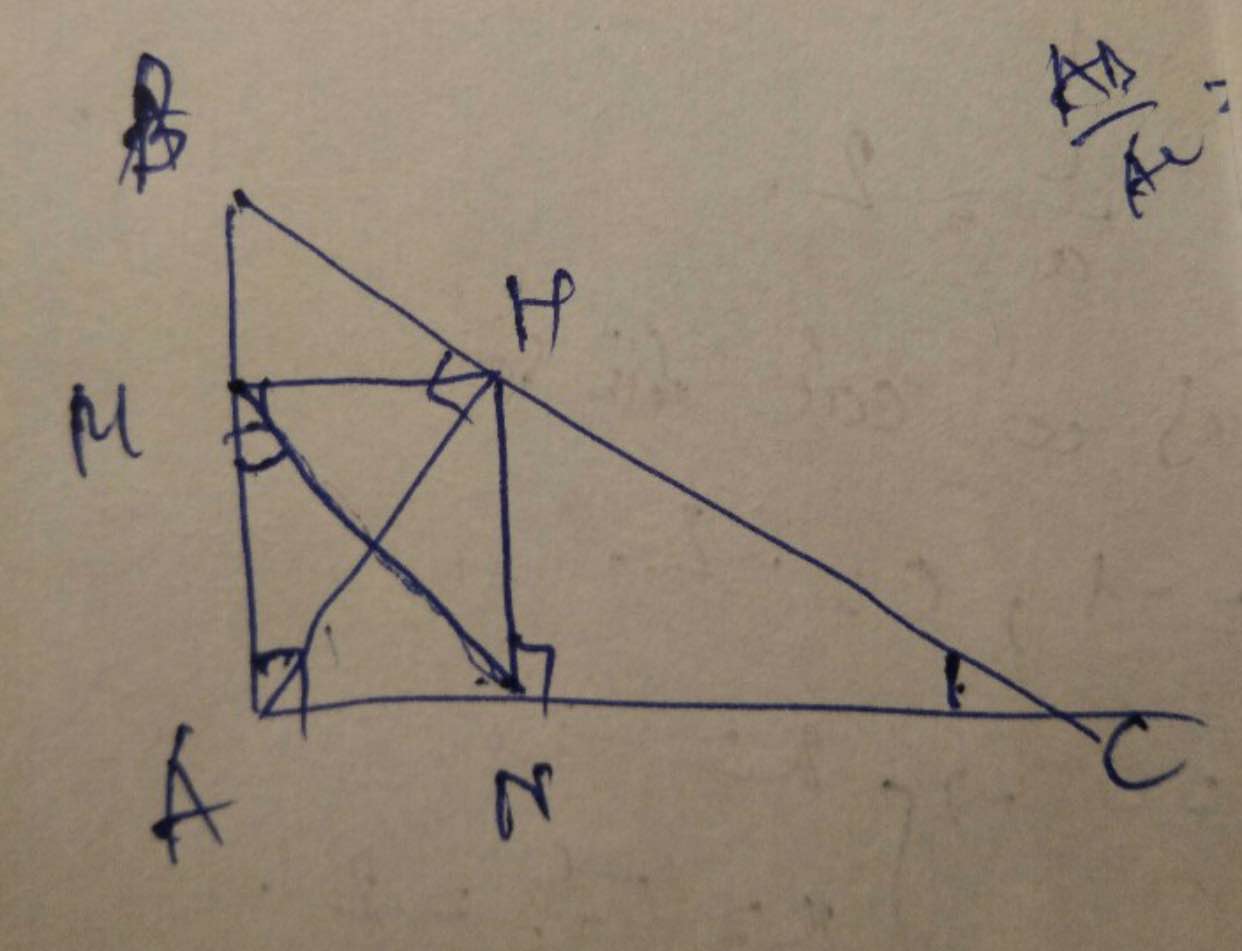
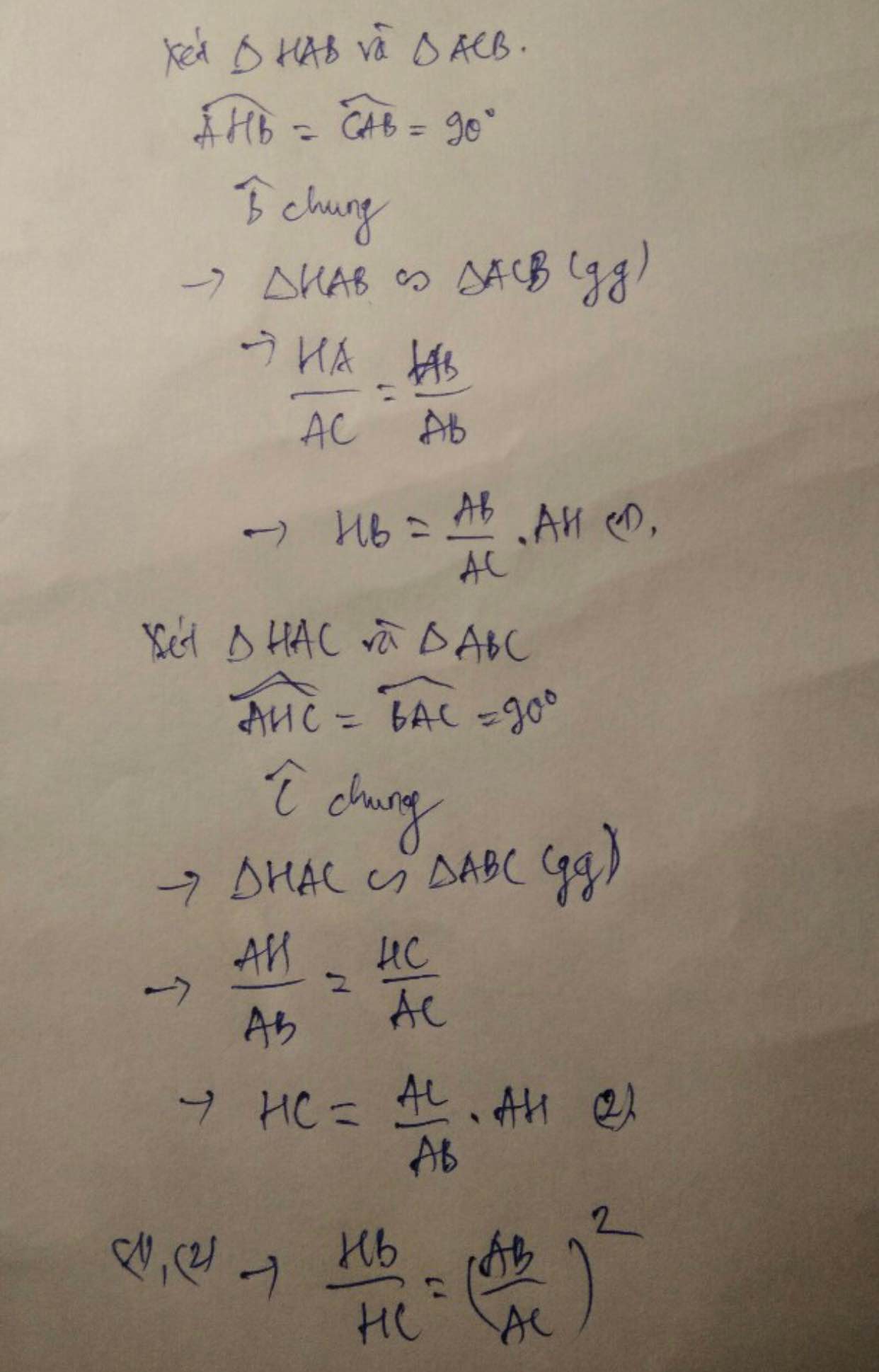
Ta thấy 1 cặp tam giác đồng dạng quen thuộc là \(\Delta HAB~\Delta HCA\), từ đó suy ra \(\dfrac{S_{HAB}}{S_{HCA}}=\left(\dfrac{AB}{AC}\right)^2\). Mà ta lại có \(\dfrac{S_{HAB}}{S_{HCA}}=\dfrac{HB}{HC}\) (2 tam giác có chung đường cao hạ từ A) nên suy ra đpcm.