
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

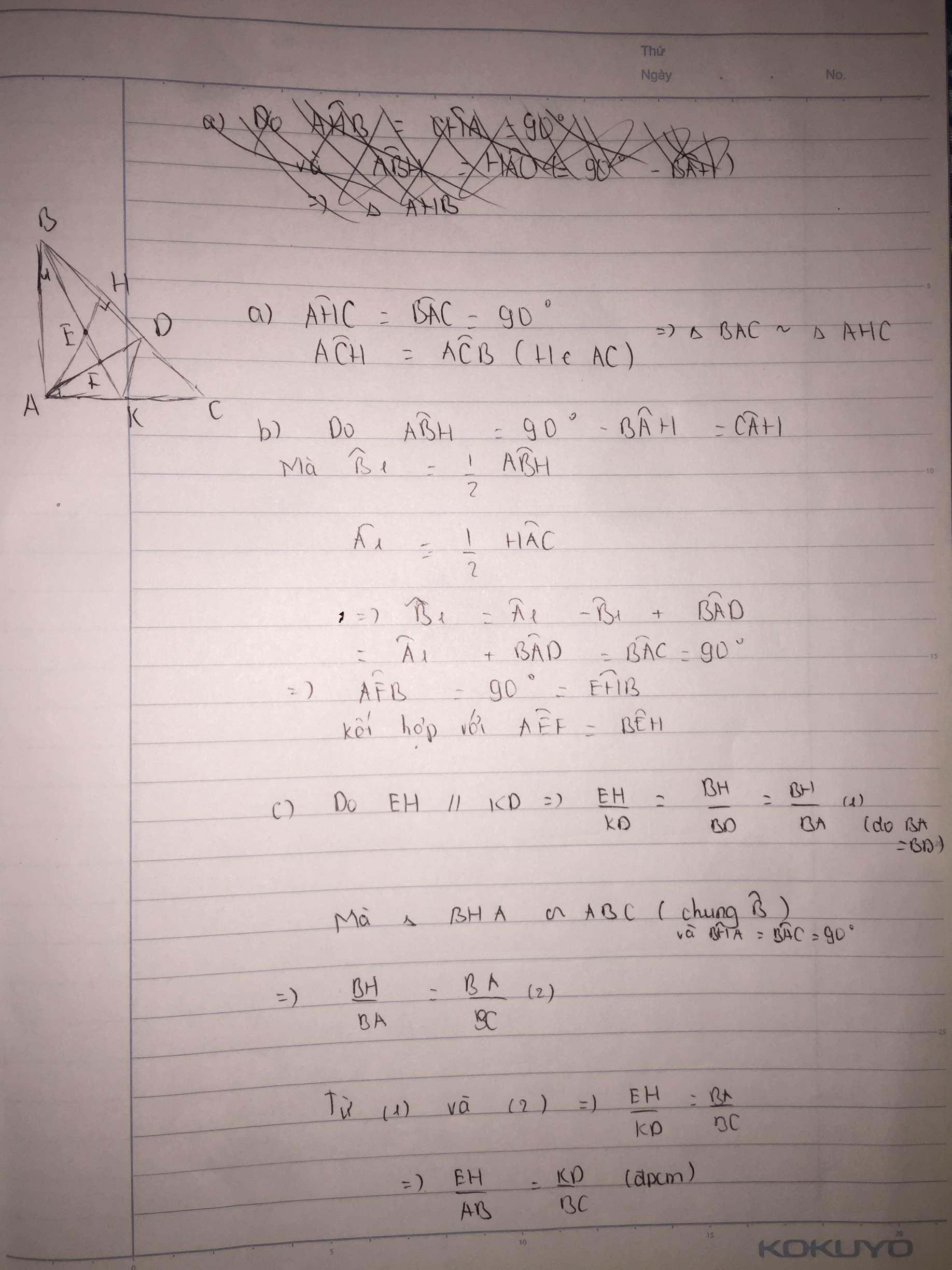

a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{CBA}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)

\(\Delta ABC\) có BK là tia phân giác
\(\Rightarrow\) \(\dfrac{KC}{KA}\) = \(\dfrac{BC}{BA}\) (1)
\(\Delta AHC\) có AD là tia phân giác
\(\Rightarrow\) \(\dfrac{DC}{DH}\) = \(\dfrac{AC}{AH}\) (2)
Xét \(\Delta ABC\) và \(\Delta HBA\) có:
góc B chung
góc BAC = BHA(=90)
\(\Rightarrow\) \(\Delta ABC\)\(\sim\)\(\Delta\)HBA (g-g)
\(\Rightarrow\) \(\dfrac{BC}{BA}\) = \(\dfrac{AC}{HA}\) (3)
Từ (1)(2)(3)\(\Rightarrow\)\(\dfrac{KC}{KA}\) = \(\dfrac{DC}{DH}\)
\(\Rightarrow\) KD//AH

hình bạn tự vé nhé.
tam giác ABC vuông tại A nên theo định lý PY-Ta-Go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=10\left(DO-BC>0\right)\)
b) xét \(\Delta ABC\) VÀ \(\Delta HBA\) CÓ:
\(\widehat{BAC}=\widehat{AHB}\)
\(\widehat{B}\) CHUNG
\(\Rightarrow\Delta ABC\) đồng dạng vs \(\Delta HBA\)
c)sửa đề:\(AB^2=BH.BC\)
TA CÓ: \(\Delta ABC\text{ᔕ}\Delta HBA\)
\(\Rightarrow\frac{AB}{BH}=\frac{BC}{AB}\left(tsđd\right)\)
\(\Rightarrow AH^2=BH.BC\)