Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
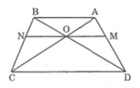
Trong ΔDAB, ta có: OM // AB (gt)
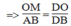(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
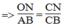(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: 
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: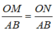 
Vậy: OM = ON
Ta có: MN // AB (gt); AB // CD(gt) => MN // AB // CD
Xét tam giác ABC có: OM // AB (MN // AB)
=> \(\dfrac{OM}{AB}=\dfrac{CM}{CA}\) (hệ quả định lý Ta lét trong tam giác) (1)
Xét tam giác ABD có: ON // AB (MN // AB)
=> \(\dfrac{ON}{AB}=\dfrac{DN}{DB}\) (hệ quả định lý Ta lét trong tam giác) (2)
Xét hình thang ABCD có: MN // AB // CD (cmt)
=> \(\dfrac{CM}{CA}=\dfrac{DN}{DB}\) (định lý Ta lét trong hình thang) (3)
Từ (1) (2) (3) => OM = ON
tham khảo :
https://lazi.vn/edu/exercise/582904/cho-hinh-thang-abcd-ab-cd-cheo-cat-nhau-tai-o-p
Xét △ADC có :MO // DC
\(\Rightarrow\frac{MO}{DC}=\frac{AO}{AC}\)(Hệ quả định lí Thales) (1)
Xét △BDC có : ON // DC
\(\Rightarrow\frac{NO}{DC}=\frac{BO}{BD}\)(Hệ quả định lí Thales) (2)
Xét △ODC có AB // DC
\(\Rightarrow\frac{AO}{AC}=\frac{BO}{BD}\)(Theo hệ quả định lí Thales) (3)
Từ (1) ; (2) và (3) :
\(\Rightarrow\frac{OM}{CD}=\frac{ON}{CD}\)
\(\Rightarrow OM=ON\left(ĐPCM\right)\)
