HK
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BM
1
25 tháng 12 2021
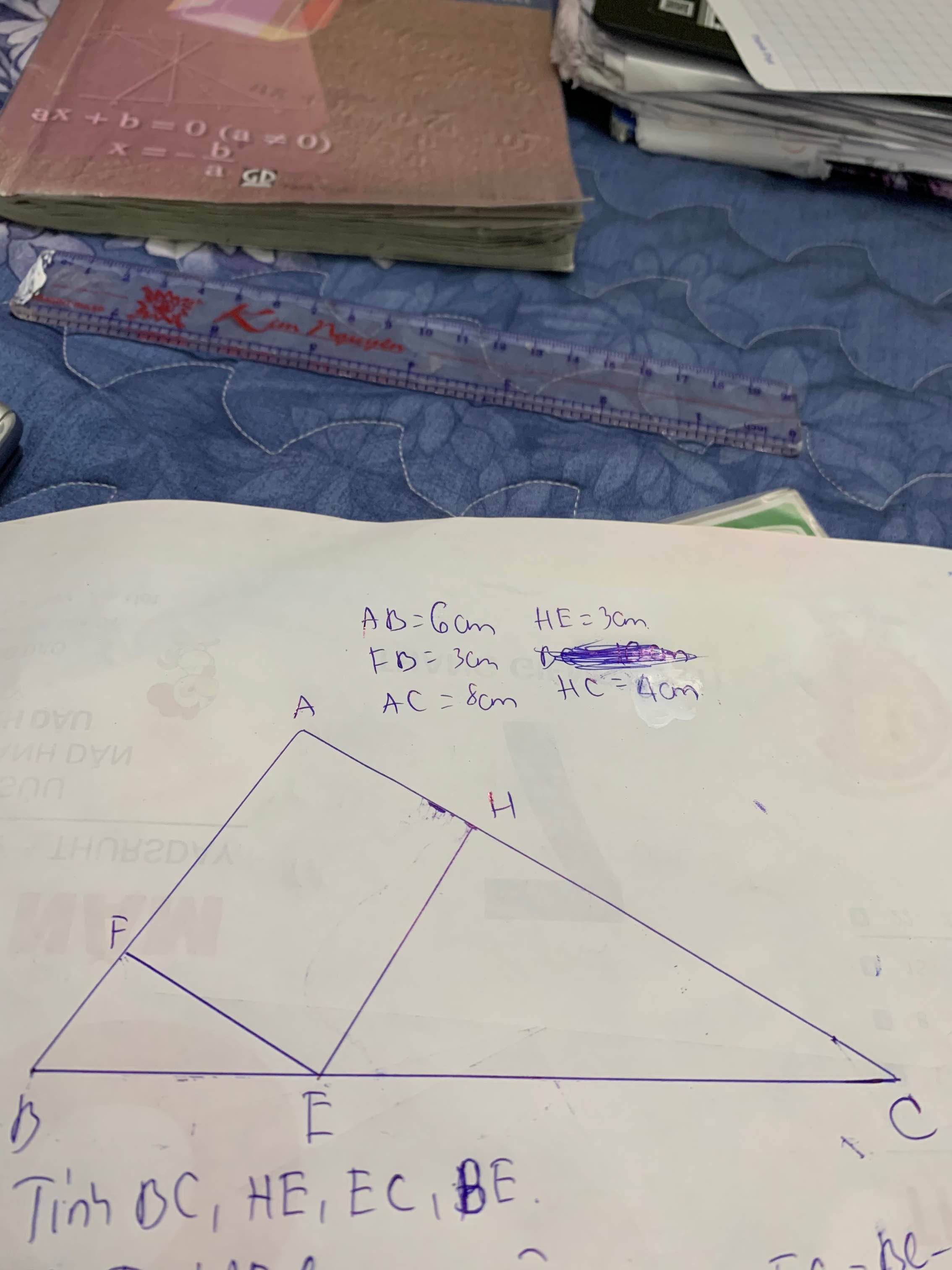
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
MS
0
KY
4
2 tháng 9 2021
b: Ta có: \(\left(x+y\right)^2-x^2+4xy-4y^2\)
\(=\left(x+y\right)^2-\left(x-2y\right)^2\)
\(=\left(x+y-x+2y\right)\left(x+y+x-2y\right)\)
\(=3y\cdot\left(2x-y\right)\)
c: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=2y^3+6x^2y\)
\(=2y\left(3x^2+y^2\right)\)
24 tháng 11 2021
Ta có : |x - 2| ; |x - 5| ; |x - 18| ≥0∀x∈R≥0∀x∈R
=> |x - 2| + |x - 5| + |x - 18| ≥0∀x∈R≥0∀x∈R
=> D có giá trị nhỏ nhất khi x = 2;5;18
Mà x ko thể đồng thời nhận 3 giá trị
Nên GTNN của D là : 16 khi x = 5 ok nha bạn
24 tháng 11 2021
x^2/x-1 = x^2-4x+4/x-1 + 4 = (x-2)^1/x-1 + 4 >= 4
Dấu "=" xảy ra <=> x-2 = 0 <=> x = 2 (tm)
Vậy GTNN của x^2/x-1 = 4 <=> x= 2
k mk nha
24 tháng 8 2021
Bài 2:
a: \(201^3=8120601\)
b: \(199^3=7880599\)
c: \(52^3-8=140600\)
d: \(23^3-27=12140\)
e: \(99^3=970299\)
f: \(62\cdot58=3596\)
24 tháng 8 2021
Bài 1:
a: \(\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=4x^2+4xy+y^2-y^2+4xy-4x^2\)
=8xy
b: \(\left(5x+5\right)^2+10\cdot\left(x-3\right)\left(x+1\right)+x^2-6x+9\)
\(=\left(5x+5\right)^2+2\cdot\left(5x+5\right)\cdot\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(6x+2\right)^2\)
\(=36x^2+24x+4\)
c: \(\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=x^3-3x^2y+3xy^2-y^3+3x^2y-3xy^2\)
\(=x^3-y^3\)
d: \(\left(1-2x\right)\left(1+2x+4x^2\right)+8\left(x-1\right)\left(x^2+x+1\right)\)
\(=1-8x^3+8\left(x^3-1\right)\)
\(=1-8x^3+8x^3-8\)
=-7
