Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a.
$(4x^2+4x+1)-x^2=0$
$\Leftrightarrow (2x+1)^2-x^2=0$
$\Leftrightarrow (2x+1-x)(2x+1+x)=0$
$\Leftrightarrow (x+1)(3x+1)=0$
$\Rightarrow x+1=0$ hoặc $3x+1=0$
$\Rightarrow x=-1$ hoặc $x=-\frac{1}{3}$
b.
$x^2-2x+1=4$
$\Leftrightarrow (x-1)^2=2^2$
$\Leftrightarrow (x-1)^2-2^2=0$
$\Leftrightarrow (x-1-2)(x-1+2)=0$
$\Leftrightarrow (x-3)(x+1)=0$
$\Leftrightarrow x-3=0$ hoặc $x+1=0$
$\Leftrightarrow x=3$ hoặc $x=-1$
c.
$x^2-5x+6=0$
$\Leftrightarrow (x^2-2x)-(3x-6)=0$
$\Leftrightarrow x(x-2)-3(x-2)=0$
$\Leftrightarrow (x-2)(x-3)=0$
$\Leftrightarrow x-2=0$ hoặc $x-3=0$
$\Leftrightarrow x=2$ hoặc $x=3$
2c.
ĐKXĐ: $x\neq 0$
PT $\Leftrightarrow x-\frac{6}{x}=x+\frac{3}{2}$
$\Leftrightarrow -\frac{6}{x}=\frac{3}{2}$
$\Leftrightarrow x=-4$ (tm)
2d.
ĐKXĐ: $x\neq 2$
PT $\Leftrightarrow \frac{1+3(x-2)}{x-2}=\frac{3-x}{x-2}$
$\Leftrightarrow \frac{3x-5}{x-2}=\frac{3-x}{x-2}$
$\Rightarrow 3x-5=3-x$
$\Leftrightarrow 4x=8$
$\Leftrightarrow x=2$ (không tm)
Vậy pt vô nghiệm.

a) \(\left(x-2\right)^2=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2-4x+4-x^2+16=0\)
\(\Leftrightarrow20-4x=0\)
\(\Leftrightarrow4x=20\)
\(\Leftrightarrow x=5\)
Vậy S = {5}
b) ĐKXĐ: \(x\ne0;x\ne-2\)
\(\dfrac{x+2}{x}=\dfrac{\left(x+1\right)\left(x+4\right)}{x^2+2x}+\dfrac{x}{x+2}\)
\(\Leftrightarrow\dfrac{x+2}{x}=\dfrac{x^2+4x+x+4+x^2}{x\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{x+2}{x}=\dfrac{2x^2+5x+4}{x\left(x+2\right)}\)
\(\Rightarrow x\left(x+2\right)^2=x\left(2x^2+5x+4\right)\)
\(\Leftrightarrow x^3+4x^2+4x=2x^3+5x^2+4x\)
\(\Leftrightarrow x^3+x^2=0\)
\(\Leftrightarrow x^2\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x+1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(TM\right)\end{matrix}\right.\)
Vậy S = {-1}
c) Câu này mình không chắc về đề lắm! Bạn dùng ô chữ M bị ngược để viết lại đề nhé!
a) Ta có: \(\left(x-2\right)^2=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2-4x+4=x^2-16\)
\(\Leftrightarrow x^2-4x+4-x^2+16=0\)
\(\Leftrightarrow-4x+20=0\)
\(\Leftrightarrow-4x=-20\)
hay x=5
Vậy: S={5}

a: \(\Leftrightarrow x^2-4-4x^2-4x-1-2x+3x^2=0\)
=>-6x-5=0
=>-6x=5
hay x=-5/6
b: \(\Leftrightarrow2x^3+8x^2+8x-8x^2-2x^3+16=0\)
=>8x+16=0
hay x=-2
c: \(\Leftrightarrow x^3-6x^2+12x-8+9x^2-1-x^3-3x^2-3x-1=0\)
=>9x-10=0
hay x=10/9
d: \(\Leftrightarrow10x-15-20x+28=19-2x^2-4x-2\)
\(\Leftrightarrow-10x+13+2x^2+4x-17=0\)
\(\Leftrightarrow2x^2-6x-4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{17}}{2}\\x_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)

\(a,8x-3=5x+12\\ \Leftrightarrow8x-5x=12+3\\ \Leftrightarrow3x=15\\ \Leftrightarrow x=\dfrac{15}{3}=5\)
\(b,x-12+4x=25+2x-1\\ \Leftrightarrow x+4x-2x=25-1+12\\ \Leftrightarrow3x=36\\ \Leftrightarrow x=\dfrac{36}{3}=12\)
\(c,7-\left(2x+4\right)=-\left(x+4\right)\\ \Leftrightarrow7-2x-4=-x-4\\ \Leftrightarrow-2x+x=-4+4-7\\ \Leftrightarrow-x=-7\\ \Leftrightarrow x=7\)
\(d,3-4x\left(45-2x\right)=8x^2+x-300\\ \Leftrightarrow3-100x+8x^2=8x^2+x-300\\ \Leftrightarrow8x^2-8x^2-100x-x=-300-3\\ \Leftrightarrow-101x=-303\\ \Leftrightarrow x=\dfrac{-303}{-101}=3\)
Đề câu d của bạn hình như sai dấu ý

Bài 1:
a:9x-6=3x+12
=>6x=18
hay x=3
b: \(\Leftrightarrow5\left(x+1\right)-8x=50\)
=>5x+5-8x=50
=>-3x+5=50
=>-3x=45
hay x=-15
c: \(\Leftrightarrow7\left(x+1\right)+2x^2=x+23\)
\(\Leftrightarrow2x^2+7x+7-x-23=0\)
\(\Leftrightarrow2x^2+6x-16=0\)
\(\Leftrightarrow x^2+3x-8=0\)
\(\text{Δ}=3^2-4\cdot1\cdot\left(-8\right)=9+32=41>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{41}}{2}\\x_2=\dfrac{-3+\sqrt{41}}{2}\end{matrix}\right.\)

\(a,x^3+x^2+x+1=0\\ \Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\\ \Rightarrow\left(x^2+1\right)\left(x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-1\right\}\)
\(b,x^3+x^2-x-1=0\\ \Rightarrow x^2\left(x+1\right)-\left(x+1\right)=0\\ \Rightarrow\left(x^2-1\right)\left(x+1\right)=0\\ \Rightarrow\left(x-1\right)\left(x+1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-1;1\right\}\)
\(c,\left(x+1\right)^2\left(x+2\right)+\left(x+1\right)^2\left(x-2\right)=-24\\ \Rightarrow\left(x+1\right)^2\left(x+2+x-2\right)=-24\\ \Rightarrow2x\left(x^2+2x+1\right)=-24\\ \Rightarrow x^3+2x^2+x+12=0\\ \Rightarrow\left(x^3+3x^2\right)-\left(x^2+3x\right)+\left(4x+12\right)=0\\ \Rightarrow x^2\left(x+3\right)-x\left(x+3\right)+4\left(x+3\right)=0\\ \Rightarrow\left(x^2-x+4\right)\left(x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-\dfrac{1}{2}\right)^2+\dfrac{15}{4}=0\left(vô.lí\right)\\x=-3\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-3\right\}\)
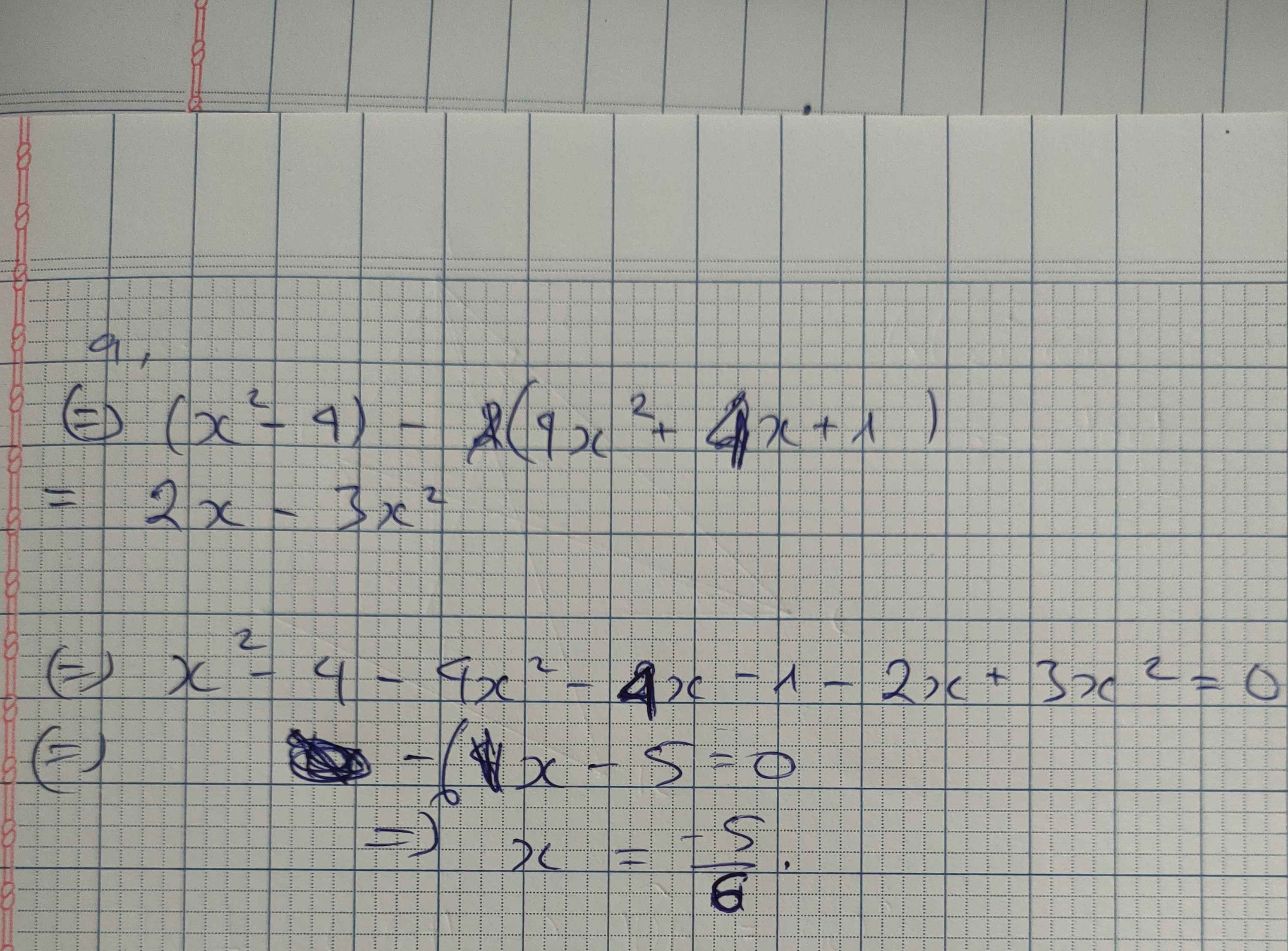
Bài b) (x-4)(x-7)(x-6)(x-5)=1680
=> (x2-11x+28)(x2-11x+30)=1680
Đặt t=x2-11x+28
=> t(t+2)=1680
=>t2+2t-1680=0
=> t2+2t+1-1681=0
=> (t+1)2-412=0
=> (t-40)(t+42)=0
=> t=40 hoặc t=-42
Bạn thế vào như câu a) để giải nhé !!!
a.X=-3
b.X=-1