Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó:ABDC là hình bình hành
Suy ra: AB//DC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao

a) Xét ΔABM và ΔDCM có
MB=MC(M là trung điểm của BC)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MA=MD(gt)
Do đó: ΔABM=ΔDCM(c-g-c)
b) Ta có: ΔABM=ΔDCM(cmt)
nên AB=CD(Hai cạnh tương ứng)
mà AB<AC(gt)
nên CD<AC
Xét ΔACD có
CD<AC(cmt)
mà góc đối diện với cạnh CD là \(\widehat{CAD}\)
và góc đối diện với cạnh AC là \(\widehat{ADC}\)
nên \(\widehat{CAD}< \widehat{ADC}\)(Định lí quan hệ giữa góc và cạnh đối diện trong tam giác)
\(\Leftrightarrow\widehat{CAM}< \widehat{MDC}\)
mà \(\widehat{BAM}=\widehat{MDC}\)(ΔABM=ΔDCM)
nên \(\widehat{BAM}>\widehat{CAM}\)(đpcm)

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB=DC
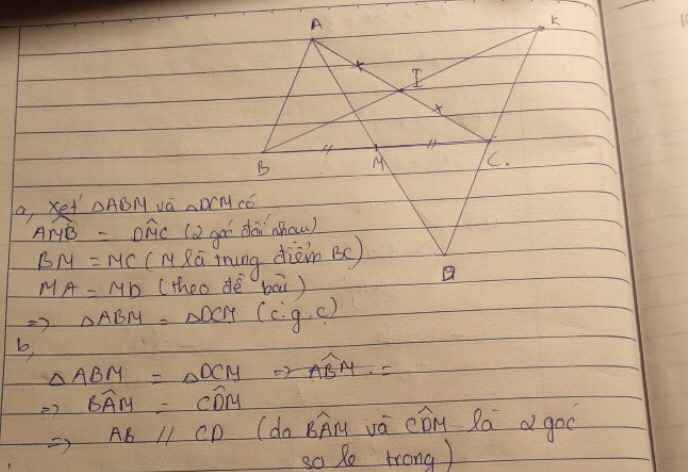
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB=DC