Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://lazi.vn/edu/exercise/cho-tam-giac-abc-co-goc-a-120-do-duong-phan-giac-ad-d-thuoc-bc-ve-de-vuong-goc-voi-ab-df-vuong-goc
a) ΔAED=ΔAFDΔAED=ΔAFD(ch-gn)nên DE=DF.(hai cạnh tương ứng)
Mặt khác dễ dàng chứng minh được EDFˆ=60o
Vì vậy tam giác DEF là tam giác đều
b)ΔEDK=ΔFDT(hai cạnh góc vuông)
nen DK=DI(hai cạnh tương ứng).Do đó Tam giác DIK cân ở D
c) AD là tia phân giác của góc BAC nên DAB^=DAC^=1/2BAC^=60o
AD//MC(gt),do đó AMCˆ=DABˆ=60o(hai góc nằm trong vị trí đồng vị)
AMC^=CAD^=60o(hai góc nằm trong vị trí sole trong)
Tam giác AMC có hai góc bằng nhau và khoảng 60o nên là tam giác đều
d)Ta có AF=AC-FC=CM-FC=m-n.


Vậy ΔDEF đều
b) Vì AD là tia phân giác của ∠BAC (gt)
⇒ ∠DAB = ∠DAC = 1/2∠BAC = 60o
Vì AD//MC (gt)
⇒ ∠AMC = ∠DAB = 60o (hai góc nằm ở vị trí đồng vị)
∠AMC = ∠CAD = 60o (hai góc nằm ở vị trí so le trong)
Xét ΔAMC có:
Hai góc bằng nhau và bằng 60o
⇒ ΔAMC đều
Vậy ΔAMC đều
Còn lại bạn tự làm nhé

a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

\(\text{#TNam}\)
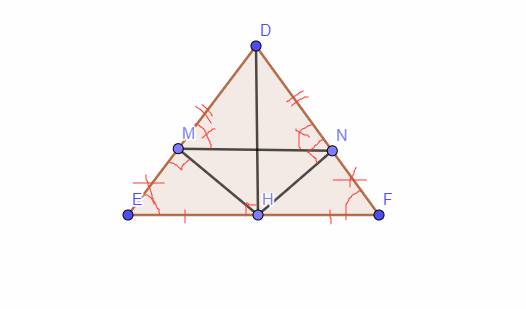
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`

a. Xét tam giác ABD và tam giác ACD
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
AD : cạnh chung
Vậy tam giác ABD = tam giác ACD ( c.g.c )
b. ta có trong tam giác ABC đường trung tuyến cũng là đường cao
=> AD vuông BC
CD = BC : 2 = 12 : 2 =6cm
c.áp dụng định lý pitago vào tam giác vuông ADC
\(AC^2=AD^2+DC^2\)
\(AD=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)
d.Xét tam giác vuông BDE và tam giác vuông CDF có:
AD = CD ( gt )
góc B = góc C
Vậy tam giác vuông BDE = tam giác vuông CDF ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
=> tam giác DEF cân tại D
a) Tam giác ABD và tam giác ACD có:
BD = CD (Vì D là trung điểm của BC)
góc B = góc C
(vì tam giác ABC cân tại A)
AB = AC
Do đó: am giác ABD = tam giác ACD (c.g.c)
Suy ra: Góc ADB = góc ADC (cặp góc t/ứng)
b) Vì góc ADB = góc ADC (cmt) mà góc ADB + góc ADC 180 độ (2 góc kề bù)
nên góc ADB = 180 độ / 2 = 90 độ => AD vuông góc với BC
c) Ta có : BD + CD = BC ( Vì D nằm giữa B và C)
mà BC = 12 cm
=> CD = 12 /2 = 6 cm
Vì AD vuông góc với BC nên tam giác ADC vuông tại D
=> AC2AC2 = AD2AD2 +CD2CD2 (Định lý Pytago)
=> 10^2 = AD ^ 2 + 6 ^2
=> AD^2 = 64
=> AD = 8 (cm) (vì AD > 0 )
d) bạn c/m cho tam giác DEB = tam giác DFC (cạnh huyền - góc nhọn) nhé
=> DE = DF (cặp cạnh tương ứng) => tam giác DEF cân tại D( đn)


tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go
bài 2 nữa ạ