Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Vì 45 chia hết cho x nên x \(\in\) Ư(45) = {1;3;5;9;15;45}
=> x \(\in\) {1;3;5;9;15;45}
b. Vì 24 chia hết cho x ; 36 chia hết cho x và 160 chia hết cho x => x \(\in\) ƯC(24;36;160} = {1;2;4}
mà x lớn nhất => x = 4

Bài 1 :
ƯC( 48 ; 79 ; 72 ) = 1
Bài 2 :
160 \(⋮\)x ; 152 \(⋮\)x ; 76 \(⋮\)x và x lớn nhất
=> x là ƯCLN(160;152;76)
Ta có :
160 = 25 . 5
152 = 23 . 19
76 = 22 . 19
=> ƯCLN(160;152;76 ) = 4
Vậy x = 4
Bài 3 :
Gọi số tổ chia đc sao cho số hs nam và nữ trong mỗi tổ = nhau là a ( a> 1 )
Theo đề bài , ta có :
28 \(⋮\)a ; 24 \(⋮\)a
=> a \(\in\)ƯC( 28 ; 24 )
Ta có :
28 = 22 . 7
24 = 23 . 3
=> ƯCLN( 28 ; 24 ) = 22 = 4
=> ƯC( 28 ; 24 ) = Ư(4) = { 1;2;4 }
=> a \(\in\){ 2 ; 4 } ( a>1 )
Vậy có 2 cách chia
C1 : Số tổ 2 ; Số hs nam : 14 ; số hs nữ : 12
C2 : Số tổ 4 ; số hs nam : 7 ; số hs nữ : 6
Vậy với cách chia thành 4 tổ thì mỗi tổ có số hs ít nhất
Bài 4 :
Ta có :
13n + 7 chia hết cho 5
=> 10n + 3n + 10 - 3 chia hết cho 5
=> 3n - 3 chia hết cho 5
=> 3(n - 1) chia hết cho 5
=> n - 1 chia hết cho 5
=> n - 1 = 5k
=> n = 5k + 1
Vậy với n = 5k + 1(k tự nhiên) thì 13n + 7 chia hết cho 5

a)144+(120-x)=-36
120-x=-36-144
120-x=-180
x=120-(-180)
x=300
vậy x=300

TL ;
a) Nếu 120 và 216 chia hết cho x thì gọi là ước chung
x thỏa mãn
x = 2 ; 3
b)
x = 1 ; 2 ; 4 ; 6 ; 8 ; 12 ; 24
x = 1 ; 2 ; 3 ; 4 ; 6 ; 9 ; 12 ; 36
x = 1 ; 2 ; 4 ; 5 ; 160 ; 8 ; 10 ; 20 ; 40 ; 50 ; 80

Do 24 chia hết cho x, 36 chia hết cho x, 160 chia hết cho x
=> x thuộc ƯC(24;36;160)
Mà x lớn nhất => x = ƯCLN(24;36;160) = 8
Vậy x = 8
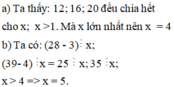
a) Các số chia hết cho:
55 là 5,10,15,20,25,30,35,...5,10,15,20,25,30,35,...
66 là 6,12,18,24,30,36,..6,12,18,24,30,36,..
1010 là 10,20,30,40,...10,20,30,40,...
→→Vậy xx nhỏ nhất để chia hết cho 5,6,105,6,10 là 30
b) 24 : x, 36 : x , 160 : x và x lớn nhất => x = ƯCLN (24, 36, 160). Vậy x = 4.