LM
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BV
6
KV
13 tháng 4 2023
Bài 1:
a) \(A\left(x\right)+B\left(x\right)=\left(-x^3+x^2-5x+1\right)+\left(x^3+4x-5\right)\)
\(=-x^3+x^2-5x+1+x^3+4x-5\)
\(=\left(-x^3+x^3\right)+x^2+\left(-5x+4x\right)+\left(1-5\right)\)
\(=x^2-x-4\)
b) \(A\left(x\right)-B\left(x\right)=\left(-x^3+x^2-5x+1\right)-\left(x^3+4x-5\right)\)
\(=-x^3+x^2-5x+1-x^3-4x+5\)
\(=\left(-x^3-x^3\right)+x^2+\left(-5x-4x\right)+\left(1+5\right)\)
\(=-2x^3+x^2-9x+6\)
KV
13 tháng 4 2023
Bài 2
* \(P+Q=\left(x^5+7x^3+1\right)+\left(x^3-4x^5+2\right)\)
\(=x^5+7x^3+1+x^3-4x^5+2\)
\(=\left(x^5-4x^5\right)+\left(7x^3+x^3\right)+\left(1+2\right)\)
\(=-3x^5+8x^3+3\)
* \(P-Q=\left(x^5+7x^3+1\right)-\left(x^3-4x^5+2\right)\)
\(=x^5+7x^3+1-x^3+4x^5-2\)
\(=\left(x^5+4x^5\right)+\left(7x^3-x^3\right)+\left(1-2\right)\)
\(=5x^5+6x^3-1\)
21 tháng 12 2021
Bài 1:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
7 tháng 11 2021
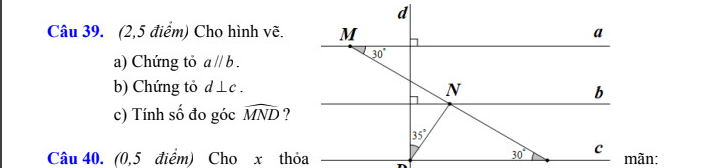
a, Vì a⊥d và b⊥d nên a//b
b, Gọi giao của MN và C là A
Ta có \(\widehat{DAM}=\widehat{AMa}=30^0\) mà 2 góc này ở vị trí SLT nên a//c
Mà a⊥d nên c⊥d
c, \(\widehat{MND}=30^0+\left(90^0-35^0\right)=85^0\)
Thi tự làm nhé
làm việc với anh Minh