
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)

Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$

5:
Th1: m=0
=>6x-27=0
=>x=27/6(loại)
TH2: m<>0
Δ=(6m-6)^2-4m(9m-27)
=36m^2-72m+36-36m^2+108m=36m+36
Để phương trình có hai nghiệm pb thì 36m+36>0
=>m>-1
x1+x2=x1x2
=>6(m-1)=9(m-3)
=>9m-27=6m-6
=>3m=21
=>m=7

22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

ĐK: \(x\ge-2\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+2}=a\ge0\\\sqrt{x^2-2x+4}=b\ge0\end{matrix}\right.\Leftrightarrow a^2+b^2=x^2-x+6\), PTTT:
\(5ab=2\left(a^2+b^2\right)\\ \Leftrightarrow2a^2-5ab+2b^2=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\2a=b\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+2=4\left(x^2-2x+4\right)\)
\(\Leftrightarrow4x^2-8x+16=x+2\\ \Leftrightarrow4x^2-9x+14=0\\ \Delta=81-224< 0\\ \Leftrightarrow x\in\varnothing\)
Với \(2a=b\Leftrightarrow4\left(x+2\right)=x^2-2x+4\)
\(\Leftrightarrow4x+8=x^2-2x+4\\ \Leftrightarrow x^2-6x-4=0\\ \Delta=36+16=52\\ \Leftrightarrow\left[{}\begin{matrix}x=3+\sqrt{13}\left(tm\right)\\x=3-\sqrt{13}\left(tm\right)\end{matrix}\right.\)
Vậy PT có nghiệm \(x=3\pm\sqrt{13}\)
Lời giải:
ĐKXĐ: $x\geq -2$
PT $\Leftrightarrow 5\sqrt{(x+2)(x^2-2x+4)}=2(x^2-x+6)$
Đặt $\sqrt{x+2}=a; \sqrt{x^2-2x+4}=b(a,b\geq 0)$ thì pt trở thành:
$5ab=2(a^2+b^2)$
$\Leftrightarrow 2a^2-5ab+2b^2=0$
$\Leftrightarrow (2a-b)(a-2b)=0$
$\Rightarrow 2a=b$ hoặc $a=2b$
Nếu $2a=b\Leftrightarrow 4a^2=b^2$
$\Leftrightarrow 4(x+2)=x^2-2x+4$
$\Leftrightarrow x=3\pm \sqrt{13}$ (tm)
Nếu $a=2b\Leftrightarrow a^2=4b^2$
$\Leftrightarrow x+2=4(x^2-x+6)$
$\Leftrightarrow 4x^2-5x+22=0$ (dễ thấy pt này vô nghiệm)


 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.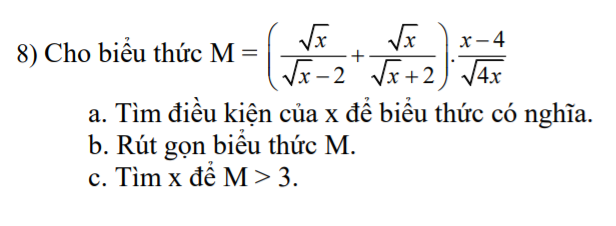


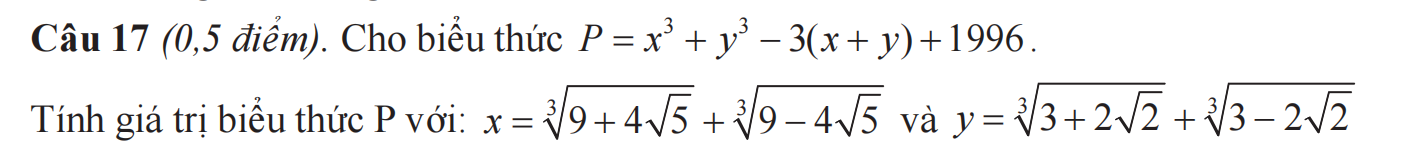 cảm ơn
cảm ơn 

\(x^2-2\left(m-2\right)x+m^2+2m-3=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ' > 0
\(\Rightarrow\left(m-2\right)^2-m^2-2m+3>0\Leftrightarrow m^2-4m+4-m^2-2m+3>0\Leftrightarrow-6m+7>0\Leftrightarrow m< \dfrac{7}{6}\)\)
Theo viét : \(\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=m^2+2m-3\end{matrix}\right.\)\)
Lại có :\( \dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{5}\)
\(\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1+x_2}{5}\)
\(\Rightarrow\left(x_1+x_2\right)\left(x_1x_2\right)=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(2m-4\right)\left(m^2+2m-3\right)=5\left(2m-4\right)\)
\(\Leftrightarrow2m^3+4m^2-6m-4m^2-8m+12=10m-20\)
\(\Leftrightarrow2m^3-24m+32=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=-4\left(n\right)\\m=2\left(l\right)\end{matrix}\right.\)
Vậy \(m=-4\) thì thỏa điều kiện
bạn quy đồng chỗ \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_2}{x_1x_2}+\dfrac{x_1}{x_1x_2}=\dfrac{x_1+x_2}{x_1x_2}\)