Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tiểu Thư họ Nguyễn Edga Trần Đăng Nhất các bn cs bt lm k Mai Hà Chi

\(\left\{{}\begin{matrix}2xy+x+2y=5\\xy+3x-3y=5\end{matrix}\right.\)
\(\Rightarrow2xy+x+2y=xy+3x-3y\)
\(\Rightarrow2xy+x+2y-xy-3x+3y=0\)
\(\Rightarrow\left(2xy-xy\right)+\left(x-3x\right)+\left(2y+y\right)=0\)
\(\Rightarrow xy-2x+3y=0\)
\(\Rightarrow xy-2x+3y-6=-6\)
\(\Rightarrow x\left(y-2\right)+3\left(y-2\right)=-6\)
\(\Rightarrow\left(x+3\right)\left(y-2\right)=-6\)
Xét ước là xong,mấy câu kia tương tự

Bài tập 2:
a/ A + (x2 - 2xy + y2) = x2 +2xy + y2
=> A = (x2 + 2xy + y2) - (x2 - 2xy + y2)
=> A = x2 + 2xy + y2 - x2 + 2xy - y2
=> A = (x2 - x2) + (2xy + 2xy) + (y2 - y2)
=> A = 0 + (2 + 2). xy + 0
=> A = 4xy
b/ B - (x2y-3xy2 +5) = 3x2 + 1 + 4x2y
=> B = (3x2 + 1 + 4x2y) + (x2y-3xy2 +5)
=> B = 3x2 + 1 + 4x2y + x2y - 3xy2 + 5
=> B = (1 + 5) + (4x2y - x2y) + 3x2 - 3xy2
=> B = 6 + 3x2y + 3x2 - 3xy2
D - 9x + 2y3 - 7x3y2 - 4x5y + 1 = 0
=> D = 0 + 9x + 2y3 - 7x3y2 - 4x5y + 1
=> D = 9x + 2y3 - 7x3y2 - 4x5y + 1
P.s: Lần sau bạn đăng 1 câu hỏi/ bài đăng thôi nhé! Và nhớ dùng công thức trực quan!

Lời giải:
$\frac{x}{y}=\frac{2}{3}\Rightarrow \frac{x}{2}=\frac{y}{3}$. Đặt $\frac{x}{2}=\frac{y}{3}=k$ thì:
$x=2k; y=3k$
Khi đó: $3x-2y=3.2k-3.2k=0$. Mẫu số không thể bằng $0$ nên $A$ không xác định. Bạn xem lại.
$B=\frac{2(2k)^2-2k.3k+3(3k)^2}{3(2k)^2+2.2k.3k+(3k)^2}=\frac{29k^2}{33k^2}=\frac{29}{33}$

suy ra x.(y-2)-3.(y-2)+6+1=0
suy ra (x-3).(y-2)=-7
suy ra x-3;y-2 thuộc Ư(-7)
tự lập bảng tự tính

Bài 1:
a) Ta có: \(2x=5y.\)
=> \(\frac{x}{y}=\frac{5}{2}\)
=> \(\frac{x}{5}=\frac{y}{2}\) và \(x.y=90.\)
Đặt \(\frac{x}{5}=\frac{y}{2}=k\Rightarrow\left\{{}\begin{matrix}x=5k\\y=2k\end{matrix}\right.\)
Có: \(x.y=90\)
=> \(5k.2k=90\)
=> \(10k^2=90\)
=> \(k^2=90:10\)
=> \(k^2=9\)
=> \(k=\pm3.\)
TH1: \(k=3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.5=15\\y=3.2=6\end{matrix}\right.\)
TH2: \(k=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).5=-15\\y=\left(-3\right).2=-6\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(15;6\right),\left(-15;-6\right).\)
e) Ta có: \(\frac{x}{y}=\frac{4}{5}.\)
=> \(\frac{x}{4}=\frac{y}{5}\) và \(x.y=20.\)
Đặt \(\frac{x}{4}=\frac{y}{5}=k\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
Có: \(x.y=20\)
=> \(4k.5k=20\)
=> \(20k^2=20\)
=> \(k^2=20:20\)
=> \(k^2=1\)
=> \(k=\pm1.\)
TH1: \(k=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=1.4=4\\y=1.5=5\end{matrix}\right.\)
TH2: \(k=-1\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-1\right).4=-4\\y=\left(-1\right).5=-5\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(4;5\right),\left(-4;-5\right).\)
Chúc bạn học tốt!

\(a.M+(5x^2-2xy)=6x^2+9xy-y^2
\)
\(M=(6x^2+9xy-y^2)-(5x^2-2xy)\)
\(M=6x^2+9xy-y^2-5x^2+2xy\)
\(M=(6x^2-5x^2)+(9xy+2xy)-y^2\)
\(M=x^2+11xy-y^2\)
Vậy \(M=x^2+11xy-y^2\)
\(b.M+(3x^2y-2xy^3)=2x^2y-4xy^3\)
\(M=(2x^2y-4xy^3)-(3x^2-2xy^3)\)
\(M=
\) \(2x^2-4xy^3-3x^2+2xy^3\)
\(M=(2x^2-3x^2)+(-4xy^3+2xy^3)\)
\(M=-x^2-2xy^3\)
Vậy \(M=-x^2-2xy^3\)
a) M + (5x\(^2\) - 2xy) = 6x\(^2\) + 9xy - y\(^2\)
=> M = (6x\(^2\) + 9xy - y\(^2\)) - (5x\(^2\) - 2xy)
M = 6x\(^2\) + 9xy - y\(^2\) - 5x\(^2\) + 2xy
M = (6x\(^2\) - 5x\(^2\)) + (9xy + 2xy) - y\(^2\)
M = 1x\(^2\) + 11xy - y\(^2\)
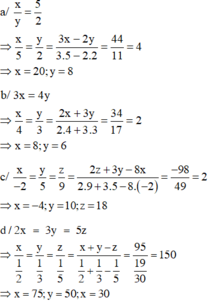
\(xy+2x+2y=-16\)
\(\Rightarrow xy+2x+2y+4=-12\)
\(\Rightarrow x\left(y+2\right)+2\left(y+2\right)=-12\)
\(\Rightarrow\left(x+2\right)\left(y+2\right)=-12\)
Xét ước 12 là xong mấy câu kia tương tự