Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

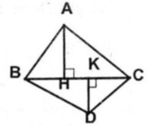
Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC

bạn gửi lại link vào chỗ tin nhắn của mk đc ko. THANKS!!!

a) Xét ΔABC có
BE là đường cao ứng với cạnh AC(gt)
CF là đường cao ứng với cạnh AB(gt)
BE cắt CF tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: AH⊥BC
b) Xét tứ giác BHCK có
HC//BK(gt)
BH//CK(gt)
Do đó: BHCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: Hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà M là trung điểm của BC(gt)
nên M là trung điểm của HK
hay H,M,K thẳng hàng(đpcm)

Ta có: AEH=90⁰.
=>HAE+AHE=90⁰.(1)
Ta có: ∆BHD vuông tại D.
=>DBH+BHD=90⁰.(2)
Từ (1) và (2) suy ra: HAE+AHE=DBH+BHD=90⁰.
Mà: AHE=DBH (2 góc đối đỉnh).
=> HAE=DBH.
=>HAE=DBE.
=>∆HEA~CBE(g.g).
=>AE/BE=HE/CE.
=>BE.HE=AE.CE.=>4BE.HE=4AE.CE.=>4BE.HE=AC².
=> (AE+CE)²=4AE.CE.
=>(AE-CE)²=0.
=>AE=CE
=> E là trung điểm của AC
=> BE là đường trung tuyến của ∆ABC
Mà: BE là đường cao của ∆ABC.
=> ∆ABC cân tại B.