
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

Xy=2(x+y)
<=> (xy-2x)-(2y-4)=4
<=>x(y-2)-2(y-2)=4
<=>(X-2)(y-2)=4=1.4=2.2
Có x,y là số nguyên dương nên x-2,y-2 là số nguyên dương lớn hơn hoặc bằng-2 nên ta có
Th1: x-2=1,y-2=4
=> X=3,y=6.
Th2: x-2=4,y-2=1
=> X=6,y=3.
Th3: x-2=y-2=2
=> X=y=4.

Xét tứ giác MECF có
ME//CF
MF//EC
Do đó: MECF là hình bình hành
Suy ra: ME=CF, MF=EC
ME+MF=CF+EC ko đổi

1. Do góc BOC kề bù với góc AOB
=> Tia OA và tia OC đối nhau
Do góc AOD và góc AOB kề bù
=> tia OD và tia OB đối nhau
=> góc BOC và góc AOD là 2 góc đối đỉnh
Gọi OM, ON là 2 tia phân giác góc AOD và góc BOC
=> góc AOM = 1/2 góc AOD = 1/2 (180* - 135*) = 45*/2
mà góc AON = góc AOB + góc BON
=> góc AON = 135* + 45*/2
=> góc AOM + góc AON = 135* + 45*/2 + 45*/2 = 180*
=> góc MON = 180*
=> OM , ON là 2 tia đối nhau

(x^2+1)(x-1)(x+3)>0
Vì x^2+1>0 với mọi x
nên: (x-1)(x+3)>0
Trường hợp 1:
x-1<0, x+3 <0
Vì x+3 > x-1 nên x+3<0 suy ra x<-3
Trường hợp 2:
x-1>0, x+3>0
Vì x-1<x+3 nên x-1 >0 suy ra x>1
Vậy x<-3 hoặc x>1
Vì tích 3 số là số dương nên trong 3 số có thể gồm 2 số âm, 1 số dương hoặc cả 3 số đều dương
TH1: Có 2 số âm, 1 số dương
Trước hết ta có \(x+3>x-1\)
\(x^2+1>x-1\)
Vì vậy \(x-1< 0\)
\(x^2+1>0\) nên \(x+3< 0\)
\(\Rightarrow x< -3\left(< 1\right)\)
TH2: Cả 3 số đều dương
Xét số bé nhất lớn hơn 0:
\(x-1>0\Rightarrow x>1\)
Vậy \(\orbr{\begin{cases}x< -3\\x>1\end{cases}}\)
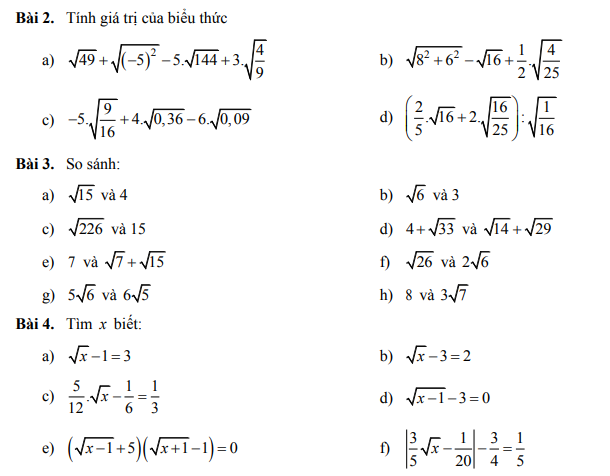 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
mk ko hiểu
đề thiếu à bạn, sao mk ko hiểu z