Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)
Do đường tròn tiếp xúc với \(d_1;d_2\) nên:
\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)
Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.
2.
Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?

Giả sử (C) tâm I ; BK R
\(I\in d':2x+y=0\) \(\Rightarrow I\left(t;-2t\right)\)
\(\Rightarrow R^2=IA^2=\left(t-4\right)^2+\left(-2t-2\right)^2\) \(=5t^2+20\)
Ta có : \(IA=\dfrac{\left|t-7.\left(-2t\right)+10\right|}{\sqrt{1+7^2}}\) \(\Rightarrow IA^2=\dfrac{\left(15t+10\right)^2}{50}=\dfrac{\left(3t+2\right)^2}{2}\)
Suy ra : \(5t^2+20=\dfrac{\left(3t+2\right)^2}{2}\) \(\Leftrightarrow10t^2+40=9t^2+12t+4\)
\(\Leftrightarrow t^2-12t+36=0\) \(\Leftrightarrow t=6\)
Suy ra : \(I\left(6;-12\right)\) ; \(R^2=200\)
PT (C) : \(\left(x-6\right)^2+\left(y+12\right)^2=200\)
Do I thuộc \(2x+y=0\) nên tọa độ có dạng \(I\left(x;-2x\right)\)
Đường thẳng \(d_1\) qua A và vuông góc (d) có pt:
\(7\left(x-4\right)+1\left(y-2\right)=0\Leftrightarrow7x+y-30=0\)
Do (C) tiếp xúc (d) tại A nên I thuộc \(d_1\)
Thay tọa độ I vào pt \(d_1\Rightarrow7x+\left(-2x\right)-30=0\Rightarrow x=6\)
\(\Rightarrow I\left(6;-12\right)\Rightarrow R^2=IA^2=200\)
Phương trình: \(\left(x-6\right)^2+\left(y+12\right)^2=200\)

Đề bài sai
Điểm \(M\left(-5;2\right)\) không thuộc \(\Delta\) nên (C) ko thể tiếp xúc với \(\Delta\) tại M
Cảm ơn thầy đã góp ý ạ, nếu đề bài đúng thì hướng làm ra sao vậy ạ?

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

Gọi pt đường tròn có dạng\(\left(C\right):\left(x-1\right)^2+\left(y+2\right)^2=R^2\)
Có \(R=d_{\left(A;d\right)}=\dfrac{\left|2.1-\left(-2\right)+6\right|}{\sqrt{2^2+1}}=\dfrac{10}{\sqrt{5}}\)
\(\Rightarrow R^2=20\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y+2\right)^2=20\)

1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

a) Gọi đường tròn cần tìm là \(\left(C\right):x^2+y^2-2ax-2by+c=0\)
\(A\left(-1;1\right)\in\left(C\right)\Rightarrow1+1+2a-2b+c=0\Rightarrow2a-2b+c=-2\)
\(B\left(3;1\right)\in\left(C\right)\Rightarrow9+1-6a-2b+c=0\Rightarrow-6a-2b+c=-10\)
\(C\left(1;3\right)\in\left(C\right)\Rightarrow1+9-2a-6b+c=0\Rightarrow-2a-6b+c=-10\)
Giải hệ phương trình ta được: \(a=1;b=1;c=-2\)
Vậy đường tròn cần tìm là: \(x^2+y^2-2x-2y-2=0\)
b) Ta có \(\left(C\right):x^2+y^2-4x+6y+3=0\)
\(\Rightarrow a=\dfrac{-4}{-2}=2;b=\dfrac{6}{-2}=-3;c=3\)
\(\Rightarrow I\left(2;-3\right)\) là tâm, bán kính \(R=\sqrt{2^2+\left(-3\right)^2-3}=\sqrt{10}\)
Để \(\left(\Delta\right)\) tiếp xúc đường tròn \(\Leftrightarrow d\left(I;\Delta\right)=R\)
\(\Leftrightarrow\dfrac{\left|9+m\right|}{\sqrt{10}}=\sqrt{10}\Leftrightarrow\left|9+m\right|=10\Leftrightarrow\left[{}\begin{matrix}9+m=10\\9+m=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-19\end{matrix}\right.\)

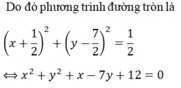
đường tròn đi qua A chứ A không phải là tâm mà
d(A, đường thẳng)=R được