Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khối lượng của hai thanh tỉ lệ theo hệ số tỉ lệ : 10/15
Gọi khối lượng hai thanh kim loại lần lượt là : x và y (gam)
⇒ x = 8,9 . 10 = 89 (gam)
y = 8,9 . 15 = 133,5 (gam)

Khối lượng của hai thanh tỉ lệ theo hệ số tỉ lệ : 10/15
Gọi khối lượng hai thanh kim loại lần lượt là : x và y (gam)
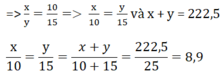
⇒ x = 8,9 . 10 = 89 (gam)
y = 8,9 . 15 = 133,5 (gam)

`a,` Gọi số đo `3` góc của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
Tỉ lệ thức biểu diễn mối quan hệ giữa số đo `3` góc trong Tam giác `ABC` là `x/2=y/3=z/4`
`b,` Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=(x+y+z)/(2+3+4)=180/9=20`
`-> x/2=y/3=z/4=20`
`->x=20*2=40, y=20*3=60, z=20*4=80`
Vậy, số đo của `3` góc trong Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0.`
a:
Đặt \(a=\widehat{A};b=\widehat{B};c=\widehat{C}\)
a/2=b/3=c/4
b: a/2=b/3=c/4=(a+b+c)/(2+3+4)=180/9=20
=>a=40; b=60; c=80

Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}=\frac{180^0}{6}=30^0\) (định lý tổng 3 góc trong tam giác)
\(\Rightarrow \widehat{A}=30^0; \widehat{B}=2.30^0=60^0; \widehat{C}=3.30^0=90^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{180}{6}=30\)
Do đó: a=30; b=60; c=90

Answer:
Ta có: Ba góc của tam giác lần lượt tỉ lệ với 1, 2, 3
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}\) và \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}=30^o\)
\(\Rightarrow\frac{\widehat{A}}{1}=30^o\Rightarrow\widehat{A}=30^o\)
\(\Rightarrow\frac{\widehat{B}}{2}=30^o\Rightarrow\widehat{B}=60^o\)
\(\Rightarrow\frac{\widehat{C}}{3}=30^o\Rightarrow\widehat{C}=90^o\)
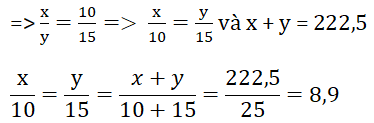

1/ Có lẽ chính xác phải là kim loại đồng nhé. Và khối lượng riêng của hai thanh là 222,5 g
Gọi m1 là khối lượng của thanh có thể tích (V1) 10 cm3 , m2 là khối lượng của thanh có thể tích (V2) 15 cm3 và
Ta có : \(m_1=V_1.225,5=10\times222,5=2225\left(g\right)\)
\(m_2=V_2.222,5=13\times222,5=2892,5\left(g\right)\)
2/ Tổng các góc của tam giác ABC là : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Áp dụng tính chất dãy tỉ số bằng nhau : \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}=\frac{180^o}{6}=30^o\)
\(\Rightarrow\begin{cases}\widehat{A}=30^o\\\widehat{B}=60^o\\\widehat{C}=90^o\end{cases}\)
m2 = 15.222,5 = 3337,5 g . (ghi lộn 13)