Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

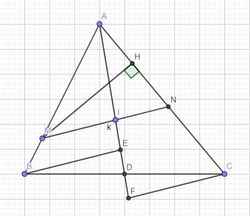
a) Bổ đề: Xét tam giác ABC cân tại A, một điểm M bất kì sao cho ^AMB = ^AMC. Khi đó MB = MC.
Bổ đề chứng minh rất đơn giản, không trình bày ở đây.
Áp dụng vào bài toán: Vì E là điểm chính giữa (BC nên EB = EC = ED => \(\Delta\)BED cân tại E
Ta có ^BAE = ^CAE (2 góc nội tiếp chắn hai cung bằng nhau) hay ^BAE = ^DAE
Áp dụng bổ đề vào \(\Delta\)BED ta được AB = AD. Khi đó AE là trung trực của BD => AE vuông góc BD
Lại có \(\Delta\)BAD ~ \(\Delta\)CFD (g.g). Mà AB = AD nên FD =FC. Từ đó EF vuông góc DC
Xét \(\Delta\)AEF có FD vuông góc AE (cmt), AD vuông góc EF (cmt) => D là trực tâm \(\Delta\)AEF (đpcm).
b) Gọi DN cắt EC tại I. Ta dễ thấy ^MDI = ^MDN = ^MBN = ^MBC = ^MEC = ^MEI
Suy ra bốn điểm D,E,M,I cùng thuộc một đường tròn => ^EMD = ^EID = 900
Nếu ta gọi MD cắt cung lớn BC của (O) tại S thì ^EMS chắn nửa (O) hay ES là đường kính của (O)
Mà E là điểm chính giữa cung nhỏ BC nên S là điểm chính giữa cung lớn BC
Do đó S là điểm cố định (Vì B,C cố định). Vậy MD luôn đi qua S cố định (đpcm).

Từ M kẻ \(MH\perp AC\Rightarrow MH=AM.sinA\)
\(S_{AMN}=\dfrac{1}{2}MH.AB=\dfrac{1}{2}AM.AN.sinA\)
Mà góc A cố định \(\Rightarrow S_{min}\) khi \(AM.AN\) đạt min
Qua B, C lần lượt kẻ các đường thẳng song song d, cắt AD tại E và F
\(\Delta BDE=\Delta CDF\left(g.c.g\right)\Rightarrow DE=DF\)
Talet: \(\dfrac{AB}{AM}=\dfrac{AE}{AI}\) ; \(\dfrac{AC}{AN}=\dfrac{AF}{AI}\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AE+AF}{AI}=\dfrac{\left(AD-DE\right)+\left(AD+DF\right)}{AI}=\dfrac{2AD}{AI}\)
Do A; I; D cố định \(\Rightarrow\dfrac{2AD}{AI}\) cố định
\(\dfrac{2AD}{AI}=\dfrac{AB}{AM}+\dfrac{AC}{AN}\ge2\sqrt{\dfrac{AB.AC}{AM.AN}}\Rightarrow AM.AN\ge\dfrac{AB.AC.AI^2}{AD^2}\)
Đẳng thức xảy ra khi và chỉ khi \(\dfrac{AB}{AM}=\dfrac{AC}{AN}\Rightarrow d||BC\) theo Talet đảo