Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{1\cdot2}>\dfrac{1}{2^2}>\dfrac{1}{2\cdot3},\dfrac{1}{2\cdot3}>\dfrac{1}{3^2}>\dfrac{1}{3\cdot4},...,\dfrac{1}{8\cdot9}>\dfrac{1}{9^2}>\dfrac{1}{9\cdot10}\)
\(\Rightarrow\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{8\cdot9}>\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}>\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{9\cdot10}\) \(\Rightarrow1-\dfrac{1}{9}>A>\dfrac{1}{2}-\dfrac{1}{10}\) \(\Rightarrow\dfrac{8}{9}>A>\dfrac{2}{5}\)

`A=(8 2/7-4 2/7)-3 4/9`
`=8+2/7-4-2/7-3-4/9`
`=4-3-4/9`
`=1-4/9=5/9`
`B=(10 2/9-6 2/9)+2 3/5`
`=10+2/9-6-2/9+2+3/5`
`=4+2+3/5`
`=6+3/5=33/5`
Bài 2:
`a)5 1/2*3 1/4`
`=11/2*13/4`
`=143/8`
`b)6 1/3:4 2/9`
`=19/3:38/9`
`=19/3*9/38=3/2`
`c)4 3/7*2`
`=31/7*2`
`=62/7`
Bài 1:
\(A=\left(8\dfrac{2}{7}-4\dfrac{2}{7}\right)-3\dfrac{4}{9}\)
\(A=\left(\dfrac{58}{7}-\dfrac{30}{7}\right)-\dfrac{31}{9}\)
\(A=4-\dfrac{31}{9}\)
\(A=\dfrac{5}{9}\)
\(B=\left(10\dfrac{2}{9}-6\dfrac{2}{9}\right)+2\dfrac{3}{5}\)
\(B=\left(\dfrac{92}{9}-\dfrac{56}{9}\right)+\dfrac{13}{5}\)
\(B=4+\dfrac{13}{5}\)
\(B=\dfrac{33}{5}\)

Ta có :
\(A=\dfrac{\dfrac{2008}{1}+\dfrac{2007}{2}+....................+\dfrac{2}{2007}+\dfrac{1}{2008}}{\dfrac{1}{2}+\dfrac{1}{3}+....................+\dfrac{1}{2008}+\dfrac{1}{2009}}\)
\(\Rightarrow A=\dfrac{\left(\dfrac{2007}{2}+1\right)+.....+\left(\dfrac{2}{2007}+1\right)+\left(\dfrac{1}{2008}+1\right)+1}{\dfrac{1}{2}+\dfrac{1}{3}+...............+\dfrac{1}{2008}+\dfrac{1}{2009}}\)
\(\Rightarrow A=\dfrac{\dfrac{2009}{2}+...................+\dfrac{2009}{2007}+\dfrac{2009}{2008}+\dfrac{2009}{2009}}{\dfrac{1}{2}+\dfrac{1}{3}+.....................+\dfrac{1}{2008}+\dfrac{1}{2009}}\)
\(\Rightarrow A=\dfrac{2009\left(\dfrac{1}{2}+..........................+\dfrac{1}{2008}+\dfrac{1}{2009}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+............................+\dfrac{1}{2008}+\dfrac{1}{2009}}\)
\(\Rightarrow A=2009\)

\(a,\dfrac{3}{5}+\dfrac{-5}{9}=\dfrac{27-25}{45}=\dfrac{2}{49}.\)
\(c,\dfrac{-27}{23}+\dfrac{5}{21}+\dfrac{4}{23}+\dfrac{16}{21}+\dfrac{1}{2}=\dfrac{-23}{23}+\dfrac{21}{21}+\dfrac{1}{2}=-1+1+\dfrac{1}{2}=\dfrac{1}{2}.\)
\(d,\dfrac{-8}{9}+\dfrac{1}{9}.\dfrac{2}{9}+\dfrac{1}{9}.\dfrac{7}{9}=\dfrac{-8}{9}+\dfrac{1}{9}.\left(\dfrac{2}{9}+\dfrac{7}{9}\right)=\dfrac{-8}{9}+\dfrac{1}{9}.1=\dfrac{-8+1}{9}=\dfrac{-7}{9}.\)

a) `1/3 - 1/4 : 2/5 = 1/3 - 5/8 = -7/24`
b) `6/7-(5/6+1/3)-(2/3+1/7) = 6/7-5/6-1/3-2/3-1/7`
`=(6/7-1/7)-(1/3+2/3)-5/6`
`=5/7-1-5/6`
`=-47/42`
c) `-5/9 . 2/5 + 4 5/9 + 5/9 . (-3/5)`
`= -5/9 . 2/5 + 4 + 5/9 + (-5/9) . 3/5`
`=-5/9 . (2/5 + 3/5-1) + 4`
`=-5/9 . 0 +4`
`=4`
d) 3 1/2 - (5 4/7 - 1 1/2) : 0,75`
`=7/2 - (39/7 - 3/2) : 3/4`
`= 7/2 - 57/14 : 3/4`
`=7/2 - 38/7`
`=-27/14`

a: \(=\dfrac{14-2+9}{32}\cdot\dfrac{4}{5}=\dfrac{21}{5}\cdot\dfrac{1}{8}=\dfrac{21}{40}\)
b: \(=10+\dfrac{2}{9}+2+\dfrac{3}{5}+6+\dfrac{2}{9}=18+\dfrac{47}{45}=\dfrac{857}{45}\)
c: \(=\dfrac{3}{10}-\dfrac{12}{5}+\dfrac{1}{10}=\dfrac{4}{10}-\dfrac{12}{5}=\dfrac{2}{5}-\dfrac{12}{5}=-2\)
d: \(=\dfrac{-25}{30}\left(\dfrac{37}{44}+\dfrac{13}{44}-\dfrac{6}{44}\right)=\dfrac{-25}{30}\cdot1=-\dfrac{5}{6}\)
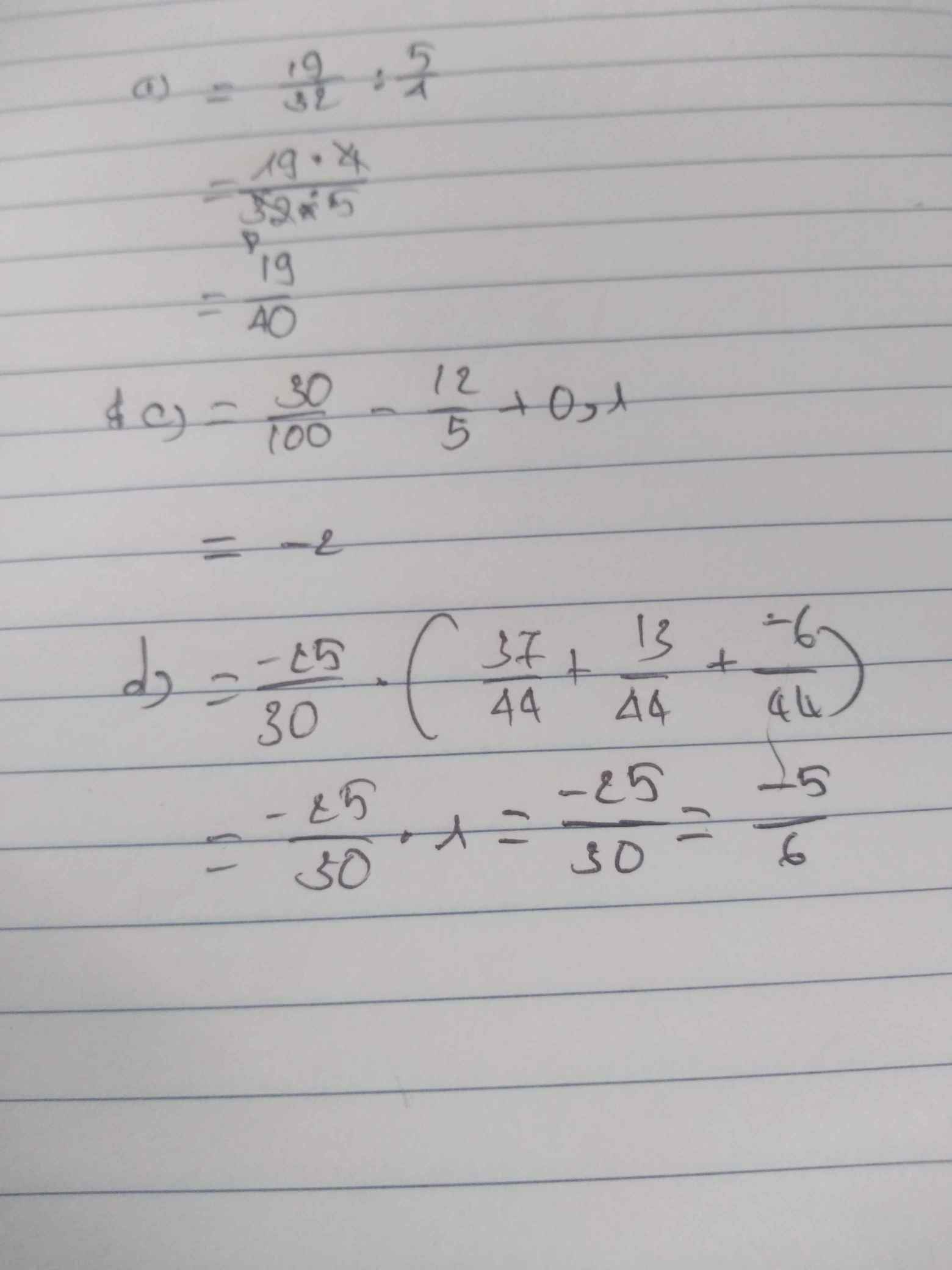
Câu 1.8: Giải
*Ta có: \(\dfrac{1}{2^2}=\dfrac{1}{2.2}>\dfrac{1}{2.3}\)
\(\dfrac{1}{3^2}=\dfrac{1}{3.3}>\dfrac{1}{3.4}\)
...
\(\dfrac{1}{9^2}=\dfrac{1}{9.9}< \dfrac{1}{9.10}\)
\(\Rightarrow A>\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(A>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(A>\dfrac{1}{2}-\dfrac{1}{10}\)
\(A>\dfrac{2}{5}\) (1)
*Ta có: \(\dfrac{1}{2^2}=\dfrac{1}{2.2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}=\dfrac{1}{3.3}< \dfrac{1}{2.3}\)
...
\(\dfrac{1}{9^2}=\dfrac{1}{9.9}< \dfrac{1}{8.9}\)
\(\Rightarrow A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{8.9}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
\(A< 1-\dfrac{1}{9}\)
\(A< \dfrac{8}{9}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{2}{5}< A< \dfrac{8}{9}\)