Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần vẽ đồ thị với lập phương trình trên hệ trục tọa độ bạn tự làm đi nhé.Ở đây ko làm đc. Phần b:
Khi 2 xe gặp nhau:Xe 1 đi được:S1=v1.t=60t(km)
Xe 2 đi được:S2=v2.t=40t(km)
Ta có:S1+S2=S↔60t+40t=100↔t=1(h)
⇒2 xe gặp nhau lúc 9 giờ
⇒2 xe gặp nhau tại vị trí cách A:S1=60.1=60(km)

Chọn trục Ox trùng với đường thẳng Hà Nội - Hải Phòng. Gốc O tại Hà Nội.
Chiều dương từ Hà Nội đến Hải Phòng. Gốc thời gian là lúc 8 giờ.
Chú ý: 15 phút=0,25 giờ; 30 phút = 0,5 giờ.
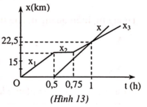
Phương trình chuyển động của xe máy có 3 giai đoạn:
- Giai đoạn 1: x 1 = 30 t (km); Điều kiện: 0 ≤ t ≤ 0 , 5 .
- Giai đoạn 2: x 2 = 15 (km)= const; Điều kiện: 0 , 5 ≤ t ≤ 0 , 75 .
- Giai đoạn 3: x 3 = 15 + 30 t − 0 , 75 (km); Điều kiện: t ≥ 0 , 75 .
Phương trình chuyển động của ô tô: t ≥ 0 , 75 (km) với t ≥ 0 , 5.
Đồ thị chuyển động của hai xe biểu diễn như hình 13.
Trên đồ thị, ô tô đuổi kịp xe máy tại thời điểm t = 1 h ( tức là lúc 9 giờ ).
Vị trí gặp nhau, cách Hà Nội 22,5km.

Vận tốc TB của ô tô:
\(v_{tb}=\dfrac{\dfrac{50}{4}+\dfrac{40}{2}+\dfrac{20}{4}}{1}=37,5\left(\dfrac{km}{h}\right)\)

a, Phương trình chuyển động của ô tô:
\(x=50t\left(km,h\right)\)
c, Thời gian ô tô từ Hà Nội đến Hải Phòng là:
\(t=\dfrac{100}{50}=2\left(h\right)\)
Vậy thời điểm ô tô tới Hải Phòng là 8+2 =10(h)
b,

Giải: Theo bài ra ta có
Quãng đường đi đầu chặng: S 1 = v 1 . t 4 = 12 , 5 t
Quãng đường chặng giữa: S 2 = v 2 . t 2 = 20 t
Quãng đường đi chặng cuối: S 1 = v 1 . t 4 = 5 t
Vận tốc trung bình:
v t b = S 1 + S 2 + S 3 t = 12 , 5 t + 20 t + 5 t t = 37 , 5 k m / h

Vận tốc trung bình của ô tô là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{s}{\dfrac{s}{2v_1}+\dfrac{s}{2v_2}}=\dfrac{2v_1v_2}{v_1+v_2}=\dfrac{2.40.60}{40+60}=48\left(km/h\right)\)