Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của người đi xe đạp lúc đầu là x(x>0)
Thời gian dự định đi hết quãng đường AB là : \(\frac{30}{x}\left(h\right)\)
Thời gian người đó đi hết nửa quãng đường đầu là : \(\frac{15}{x}\left(h\right)\)
Thời gian người đó đi hết nửa quãng đường sau là : \(\frac{15}{x+2}\left(h\right)\)
15 phút=\(\frac{1}{4}\)h Ta có:
\(\frac{30}{x}=\frac{15}{x}+\frac{1}{4}+\frac{15}{x+2}\)
\(\Leftrightarrow\frac{15}{x}-\frac{15}{x+2}=\frac{1}{4}\)
\(\Leftrightarrow\frac{1}{x}-\frac{1}{x+2}=\frac{1}{60}\)
\(\Leftrightarrow\frac{2}{x\left(x+2\right)}=\frac{1}{60}\)
\(\Leftrightarrow x\left(x+2\right)=120\)
\(\Leftrightarrow\orbr{\begin{cases}x=-12\\x=10\end{cases}\Rightarrow x=10}\)

Gọi vận tốc xe đạp là x, xe ô tô là y ( DK: y>x, x,y: dương )
Theo đề cho vận tốc xe otô lớn hơn vận tốc xe đạp là 18km/h, ta có phương trình
y - x = 18 ( 1 )
Lại có khi 2 xe gặp nhau tại C, xe đạp phải mất 4h nữa mới đến B, ta có phương trình
y + 4x = 108 ( 2 )
Từ ( 1 ) và ( 2 ) ta có hệ phương trình :
y - x = 18 và y + 4x = 108 , giải ra ta được x = 18, y = 36 ( TMĐK )
Vậy vận tốc xe đạp là 18( km / h ), Ô tô là 36 ( km / h )
Gọi vận tốc xe đạp là x, xe ô tô là y ( DK: y>x, x,y: dương )
Theo đề cho vận tốc xe otô lớn hơn vận tốc xe đạp là 18km/h, ta có phương trình
y - x = 18 ( 1 )
Lại có khi 2 xe gặp nhau tại C, xe đạp phải mất 4h nữa mới đến B, ta có phương trình
y + 4x = 108 ( 2 )
Từ ( 1 ) và ( 2 ) ta có hệ phương trình :
y - x = 18 và y + 4x = 108 , giải ra ta được x = 18, y = 36 ( TMĐK )
Vậy vận tốc xe đạp là 18( km / h ), Ô tô là 36 ( km / h )

Đổi \(30p=\frac{1}{2}h\)
Gọi vận tốc dự định của người đó là x (km/h) (x > 0)
\(\Rightarrow\) thời gian dự định của người đó là : \(t_{dđ}=\frac{S_{AB}}{v_{dđ}}=\frac{50}{x}\) (h)
Quãng đường ng đó di chuyển được sau 2 giờ là : \(2x\) (km)
\(\Rightarrow\)Quãng đường còn lại là \(50-2x\) (km)
Người đó phải tăng vận tốc thêm 2km/h trên quãng đường còn lại để đến B đúng dự định nên ta có PT :
\(\frac{50}{x}=2+\frac{1}{2}+\frac{50-2x}{x+2}\)
\(\Leftrightarrow\frac{50}{x}=\frac{5}{2}+\frac{50-2x}{x+2}\)
\(\Leftrightarrow\frac{50}{x}=\frac{5x+10+100-4x}{2\left(x+2\right)}\Leftrightarrow\frac{50}{x}=\frac{x+110}{2x+4}\)
\(\Leftrightarrow x^2+110x-100x-200=0\)
\(\Leftrightarrow x^2+10x-200=0\)
\(\Leftrightarrow\left(x-10\right)\left(x+20\right)\Rightarrow\orbr{\begin{cases}x=10\\x=-20\left(l\right)\end{cases}}\)
Vậy vận tốc ban đầu của xe là 10 km/h
Quãng đường AB dài là:
60 x 2 = 120 (km)
Nếu người đó đi với vận tốc 40km/h thì cần thời gian là:
120: 40 = 3 giờ

Gọi x(km/h) là vận tốc ban đầu của người đó(Điều kiện: x>0)
Thời gian dự định của người đó là: \(\dfrac{50}{x}\)(h)
Sau 2h30', người đó đi được: 2,5x(km)
Thời gian thực tế của người đó là: \(2+\dfrac{1}{2}+\dfrac{50-2.5x}{x+2}=\dfrac{5}{2}+\dfrac{50-2.5x}{x+2}\)
Theo đề, ta có phương trình:
\(\dfrac{5}{2}+\dfrac{50-2.5x}{x+2}=\dfrac{50}{x}\)
\(\Leftrightarrow\dfrac{5x\left(x+2\right)}{2x\left(x+2\right)}+\dfrac{2x\left(50-2.5x\right)}{2x\left(x+2\right)}=\dfrac{100\left(x+2\right)}{2x\left(x+2\right)}\)
Suy ra: \(5x^2+10x+100x-5x^2=100x+200\)
\(\Leftrightarrow10x=200\)
hay x=20(thỏa ĐK)
Vậy: vận tốc ban đầu là 20km/h

Gọi vận tốc ban đầu là x>0 (km/h)
Thời gian dự định: \(\dfrac{50}{x}\) giờ
Quãng đường đi trong 2h đầu: \(2x\) (km)
Quãng đường còn lại: \(50-2x\)
Vận tốc trên đoạn đường còn lại: \(x+2\)
Thời gian đi hết đoạn đường còn lại: \(\dfrac{50-2x}{x+2}\)
Theo bài ra ta có pt:
\(\dfrac{50}{x}=\dfrac{5}{2}+\dfrac{50-2x}{x+2}\)
\(\Leftrightarrow x^2+10x-200=0\Rightarrow\left[{}\begin{matrix}x=10\\x=-20\left(loại\right)\end{matrix}\right.\)

Gọi vận tốc dự định đi của người đó là x (km/h) (x > 0)
Thời gian dự định đi của người đó là 36/x (h)
Thời gian người đó đi nửa quãng đường đầu là 18/x (h)
Nửa quãng đường sau người đó đi với vận tốc là x + 2 (km/h) và thời gian người đó đi là 18/(x+2) (h)
Vì nghỉ lại 30 phút nên thời gian đi từ lúc xuất phát đến khi tới B là 18 x + 1 2 + 18 x + 2
Do người đó đến B chậm hơn dự kiến 12 phút = 1/5h nên ta có phương trình:
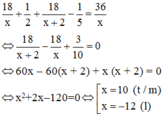
Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB là 12 km/h
Đáp án: A

gọi vận tốc bạn đầu là: x (km/h; x>0); thời gian đến B dự định: 36/x
=> vận tốc nửa đường cong lại: x+2
36:2=18 km. đổi: 18'=3/10 h
thời gian đi nửa S đầu: 18/x (h)
thời gian đi nửa S sau: 18/x+2
vì người đó đến B đúng với dự định nên ta có pt:
\(\frac{18}{x}+\frac{18}{x+2}+\frac{3}{10}=\frac{36}{x}\Leftrightarrow\frac{18x+36+18x-36x-72}{x\left(x+2\right)}=-\frac{3}{10}\Leftrightarrow-3x^2-6x+360=0\)
\(\Leftrightarrow x^2+2x-120=0\Leftrightarrow\left(x-10\right)\left(x+12\right)=0\)
=> x=10 (t/m đk) hoặc x=-12 (k t/m đk)
=> vận tốc dđ là: 10 km/h
Gọi vận tốc ban đầu của người đó là a(km/h) \((a>0)\)
Theo đề,ta có: \(\dfrac{48}{a}+\dfrac{2}{13}+\dfrac{48}{a+2}=\dfrac{96}{a}\)
\(\Leftrightarrow\dfrac{48}{a}=\dfrac{2a+628}{13\left(a+2\right)}\Leftrightarrow624a+1248=2a^2+628a\)
\(\Leftrightarrow2a^2+4a-1248=0\Rightarrow a^2+2a-624=0\)
\(\Leftrightarrow\left(a+26\right)\left(a-24\right)=0\) mà \((a>0)\Rightarrow a=24\)
\(\Rightarrow\) thời gian lăn bánh là \(\dfrac{96}{24}-\dfrac{2}{13}=\dfrac{50}{13}\left(h\right)\)