Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên \(\Delta ABC\) cân tại A.
Lại có AO là tia phân giác của góc A nên \(AO\perp BC\) (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét tam giác CBD có :
CI = IB
CO = OD (bán kính)
=> BD // HO (HO là đường trung bình của BCD) => BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
AC2 = OA2 – OC2 = 42 – 22 = 12
\(\Rightarrow AC=\sqrt{12}=2\sqrt{3}\left(cm\right)\)
Và \(\sin\widehat{OAC}=\frac{OC}{OA}=\frac{2}{4}=\frac{1}{2}\Rightarrow=\widehat{OAC}=30^o\)
Do đó \(\widehat{BAC}=2\widehat{OAC}=60^o\)
Tam giác ABC cân có \(\widehat{A}=60^o\)nên là tam giác đều
Do đó : \(AB=BC=AC=2\sqrt{3}\left(cm\right)\)

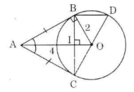
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
A C 2 = O A 2 – O C 2 = 4 2 – 2 2 = 12
=> AC = √12 = 2√3 (cm)
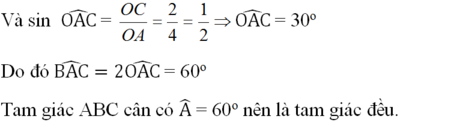
Do đó AB = BC = AC = 2√3 (cm).

a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc với BC
b: Xét (O) có
ΔCBD nội tiếp
CD là đường kính
Do đó: ΔCBD vuông tai B
=>BD//OA

Sửa đề: Cho đường tròn(O) có A là điểm nằm bên ngoài đường tròn
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: OB=OC và AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC(đpcm)
b) Xét (O) có
ΔDBC nội tiếp đường tròn có DC là đường kính
nên ΔDBC vuông tại B(Định lí)
⇒DB⊥BC
Ta có: DB⊥BC(cmt)
AO⊥BC(cmt)
Do đó: DB//AO(Định lí 1 từ vuông góc tới song song)