So sánh
A = \(\dfrac{2022^{2023}+1}{2022^{2024}+1}\) và B = \(\dfrac{2022^{2022}+1}{2022^{2023}+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


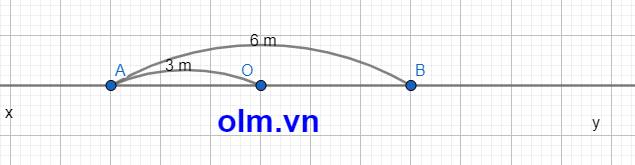
a, Các cặp tia đối nhau chung gốc A lần lượt là:
Ax và AO; Ax và AB; Ax và AY
b, Vì OA và OB là hai tia đối nhau nên O nằm giữa A và B
⇒ OA + OB = AB
⇒ OB = AB - OA
Độ dài đoạn OB là: 6 - 3 = 3 (cm)
c, Vì O nằm giữa A và B mà OA = OB = 3 cm nên O là trrung điểm AB

`@` `\text {Ans}`
`\downarrow`
`xy100(z+1)`
`= (xy100)*z + xy100`
`= xyz100 + xy100`
Vì đa thức là tổng của những đơn thức bao gồm biến và hệ số
Vậy, biểu thức trên là đa thức.


`@` `\text {Ans}`
`\downarrow`
`0,3x+1,2=2/3x+9/10`
`=> 0,3x + 1,2 - 2/3x - 9/10 = 0`
`=> (0,3-2/3)x + (1,2-9/10) = 0`
`=> (-11/30x) + 3/10 = 0`
`=> -11/30x = -3/10`
`=> x = -3/10 \div (-11/30)`
`=> x = 9/11`
Vậy, `x=9/11`
`@` `\text {Kaizuu lv uuu}`
Áp dụng phương pháp chuyển vế đổi dấu, em chuyển tất cả các hạng tử chứa ẩn \(x\) sang một bên, các hạng tử không chứa \(x\) sang một bên, đồng thời đổi dấu các hạng tử vừa chuyển.
0,3\(x+1,2=\dfrac{2}{3}x+\dfrac{9}{10}\)
\(\dfrac{2}{3}x-0,3x=1,2-\dfrac{9}{10}\)
\(\left(\dfrac{2}{3}-0,3\right)x\) = 0,3
\(\dfrac{11}{30}x\) = 0,3
\(x\) = 0,3 : \(\dfrac{11}{30}\)
\(x\) = \(\dfrac{9}{11}\)

a) Để tính số viên gạch cần sử dụng, ta cần biếtện tích của căn phòng. Diện tích của căn phòng hình chữ nhật được tính bằng cách nhân chiều dài với chiều rộng:
Diện tích = 8m x 6m = 48m²
Vì gạch hình vuông có cạnh dài 40cm, tức là có diện tích là 0.4m x 0.4m = 0.16m².
Số viên gạch cần sử dụng = Diện tích căn phòng / Diện tích một viên gạch = 48m² / 0.16m² = 300 viên gạch.
Vậy bác anh cần sử dụng 300 viên gạch để lát hết nền phòng.
b) Để tính số tiền bác anh cần phải trả, ta cần biết tổng diện tích của căn phòng. Diện tích của căn phòng đã được tính ở câu a) là 48m².
Tiền gạch cho mỗi mét vuông là 150000 đồng, tức là tiền gạch cho 1m² là 150000 đồng.
Số tiền bác anh cần phải trả = Diện tích căn phòng x Tiền gạch cho mỗi mét vuông = 48m² x 150000 đồng/m² = 7200000 đồng.
Vậy bác anh cần phải trả 720 tick mik nha

3²ˣ⁺¹ + 2.3¹⁸ = 5.3¹⁸
3²ˣ⁺¹ = 5.3¹⁸ - 2.3¹⁸
3²ˣ⁺¹ = 3¹⁸.(5 - 2)
3²ˣ⁺¹ = 3¹⁸.3
3²ˣ⁺¹ = 3¹⁹
⇒ 2x + 1 = 19
2x = 19 - 1
2x = 18
x = 9

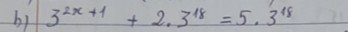
Trước hết ta phải chứng minh \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).
Thật vậy, \(\dfrac{a}{b}=\dfrac{a\left(b+1\right)}{b\left(b+1\right)}=\dfrac{a+ab}{b^2+b}\) và \(\dfrac{a+1}{b+1}=\dfrac{\left(a+1\right)b}{\left(b+1\right)b}=\dfrac{ab+b}{b^2+b}\).
Mà theo giả thuyết là a < b nên \(\dfrac{a+ab}{b^2+b}< \dfrac{ab+b}{b^2+b}\), suy ra \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).
Từ đây ta có:
\(B=\dfrac{2022^{2022}+1}{2022^{2023}+1}=\dfrac{2022^{2023}+2022}{2022^{2024}+2022}=\dfrac{2022^{2023}+2021+1}{2022^{2024}+2021+1}\)
Đặt \(A_1=\dfrac{2022^{2023}+2}{2022^{2024}+2}=\dfrac{2022^{2023}+1+1}{2022^{2024}+1+1}\), rõ ràng \(A_1>A\).
Đặt \(A_2=\dfrac{2022^{2023}+3}{2022^{2024}+3}=\dfrac{2022^{2023}+2+1}{2022^{2024}+2+1}\), rõ ràng \(A_2>A_1\).
...
Đặt \(A_{2020}=\dfrac{2022^{2023}+2021}{2022^{2024}+2021}=\dfrac{2022^{2023}+2020+1}{2022^{2024}+2020+1}\), rõ ràng \(A_{2020}>A_{2019}\) và \(B>A_{2020}\).
Suy ra \(B>A_{2020}>A_{2019}>...>A_2>A_1>A\). Vậy A < B.
Ta có A = \(\dfrac{2022^{2023}}{2022^{2024}}=\dfrac{1}{2022}\) ; B = \(\dfrac{2022^{2022}}{2022^{2023}}=\dfrac{1}{2022}\)
Mà \(\dfrac{1}{2022}=\dfrac{1}{2022}\)
Vậy A = B