sin63o = coso.
cos78o = sino.
tan53o = coto.
cot68o = tano.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác \(AHB\)vuông tại \(H\)đường cao \(HD\):
\(AH^2=AD.AB\)(hệ thức trong tam giác vuông)
Tương tự \(AH^2=AE.AC\).
Suy ra \(AD.AB=AE.AC\).
b) \(AD.AB=AE.AC\Leftrightarrow\frac{AD}{AC}=\frac{AE}{AB}\)
Xét tam giác \(AED\)và tam giác \(ABC\):
\(\widehat{A}\)chung
\(\frac{AD}{AC}=\frac{AE}{AB}\)
suy ra \(\Delta AED~\Delta ABC\left(c.g.c\right)\)
suy ra \(\widehat{AED}=\widehat{ABC}\).
Xét tam giác AHC đường cao HE
\(AH^2=AE.AC\)( hệ thức lượng ) (1)
Xét tam giác AHB đường cao HD
\(AH^2=AD.AB\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra : \(AE.AC=AD.AB\)ps : mình sửa đề luôn
b, Xét tam giác AED và tam giác ABC ta có :
^A _ chung
\(AE.AC=AD.AB\)( cmt ) \(\Rightarrow\frac{AE}{AB}=\frac{AD}{AC}\)( tỉ lệ thức )
Vậy tam giác AED ~ tam giác ABC ( c.g.c )
=> ^AED = ^ABC ( 2 góc tương ứng )

Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=144+256=400\Rightarrow BC=20\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{144}{20}=\frac{36}{5}\)cm
\(\Rightarrow HC=BC-HB=20-\frac{36}{5}=\frac{64}{5}\)cm
Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{20}{12+16}=\frac{20}{28}=\frac{5}{7}\)
\(\Rightarrow BD=\frac{5}{7}AB=\frac{5}{7}.12=\frac{60}{7}\)cm
\(\Rightarrow HD=BD-BH=\frac{60}{7}-\frac{36}{5}=\frac{48}{35}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{192}{20}=\frac{48}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{48}{5}\right)^2+\left(\frac{48}{35}\right)^2=\frac{4608}{49}\Rightarrow AD=\frac{48\sqrt{2}}{7}\)cm

Giả sử \(a=\sqrt{3}+\sqrt{5}\inℚ\)
\(\Rightarrow a^2=3+2\sqrt{3}.\sqrt{5}+5\inℚ\)
\(\Rightarrow a^2-8=2\sqrt{15}\inℚ\)
Vô lý do \(a^2-8\inℚ;2\sqrt{15}\in I\)
Do đó \(\sqrt{3}+\sqrt{5}\)là số vô tỷ.

sửa đề : \(\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=\sqrt{5^2+2.5\sqrt{2}+2}-\sqrt{4^2+2.4\sqrt{2}+2}\)
\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}=\left|5+\sqrt{2}\right|-\left|4+\sqrt{2}\right|\)
\(=5+\sqrt{2}-4-\sqrt{2}=1\)
=1 nha
t.i.c.k mình nha
bạn nào 10sp gúp mình đi



Ta có: A = \(\frac{\sqrt{5}+3}{\sqrt{2}+\sqrt{3+\sqrt{5}}}+\frac{3-\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
\(=\frac{\sqrt{10}+3\sqrt{2}}{2+\sqrt{6+2\sqrt{5}}}+\frac{3\sqrt{2}-\sqrt{10}}{2-\sqrt{3-\sqrt{5}}}\)
\(=\frac{\sqrt{10}+3\sqrt{2}}{2+\left(1+\sqrt{5}\right)}+\frac{3\sqrt{2}-\sqrt{10}}{2-\left(\sqrt{5}-1\right)}\)
\(=\sqrt{2}+\sqrt{2}\)
\(=2\sqrt{2}\)

f(x1)=3x1f(x1)=3x1
f(x2)=3x2f(x2)=3x2
Theo giả thiết, ta có:
x1<x2⇔3.x1<3.x2x1<x2⇔3.x1<3.x2 ( vì 3>03>0 nên chiều bất đẳng thức không đổi)
⇔f(x1)<f(x2)⇔f(x1)<f(x2) (vì f(x1)=3x1;f(x1)=3x1;f(x2)=3x2)f(x2)=3x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên RR.
Chú ý:
Ta cũng có thể làm như sau:
Vì x1<x2x1<x2 nên x1−x2<0x1−x2<0
Từ đó: f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0
Hay f(x1)<f(x2)f(x1)<f(x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên R
Do \(x_1< x_2\Rightarrow3x_1< 3x_2\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Hàm số \(f\)đồng biến trên \(ℝ\)khi :
\(\forall x_1,x_2\inℝ\): \(x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
=> Hàm số đã cho đồng biến trên \(ℝ\)

+) Thay giá trị của xx vào biểu thức của hàm số y=0,5xy=0,5x, ta được:
f(−2,5)=0,5.(−2,5)=−1,25f(−2,5)=0,5.(−2,5)=−1,25.
f(−2,25)=0,5.(−2,25)=−1,125f(−2,25)=0,5.(−2,25)=−1,125.
f(−1,5)=0,5.(−1,5)=−0,75f(−1,5)=0,5.(−1,5)=−0,75.
f(−1)=0,5.(−1)=−0,5f(−1)=0,5.(−1)=−0,5.
f(0)=0,5.0=0f(0)=0,5.0=0.
f(1)=0,5.1=0,5f(1)=0,5.1=0,5.
f(1,5)=0,5.1,5=0,75f(1,5)=0,5.1,5=0,75.
f(2,2,5)=0,5.2,25=1,125f(2,2,5)=0,5.2,25=1,125.
f(2,5)=0,5.2,5=1,25f(2,5)=0,5.2,5=1,25.
+) Thay giá trị của xx vào biểu thức của hàm số y=0,5x+2y=0,5x+2, ta được:
f(−2,5)=0,5.(−2,5)+2=−1,25+2=0,75f(−2,5)=0,5.(−2,5)+2=−1,25+2=0,75.
f(−2,25)=0,5.(−2,25)+2=−1,125+2=0,875f(−2,25)=0,5.(−2,25)+2=−1,125+2=0,875.
f(−1,5)=0,5.(−1,5)+2=−0,75+2=1,25f(−1,5)=0,5.(−1,5)+2=−0,75+2=1,25.
f(−1)=0,5.(−1)+2=−0,5+2=1,5f(−1)=0,5.(−1)+2=−0,5+2=1,5.
f(0)=0,5.0+2=0+2=2f(0)=0,5.0+2=0+2=2.
f(1)=0,5.1+2=0,5+2=2,5f(1)=0,5.1+2=0,5+2=2,5.
f(1,5)=0,5.1,5+2=0,75+2=2,75f(1,5)=0,5.1,5+2=0,75+2=2,75.
f(2,2,5)=0,5.2,25+2=1,125+2=3,125f(2,2,5)=0,5.2,25+2=1,125+2=3,125.
f(2,5)=0,5.2,5+2=1,25+2=3,25f(2,5)=0,5.2,5+2=1,25+2=3,25.
Vậy ta có bảng sau:
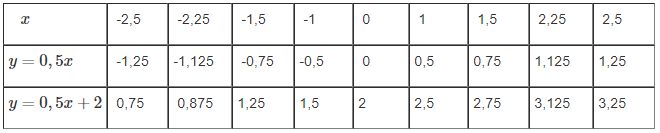
b)
Khi xx lấy cùng một giá trị của xx thì giá trị của hàm số y=0,5x+2y=0,5x+2 lớn hơn giá trị của hàm số y=0,5xy=0,5x là 22 đơn vị.
a)
| x | -2,5 | -2,25 | -1,5 | -1 | 0 | 1 | 1,5 | 2,25 | 2,5 |
| y=0,5x | -1,25 | -1,125 | -0,75 | -0,5 | 0 | 0,5 | 0,75 | 1,125 | 1,25 |
| y=0,5x+2 | 0,75 | 0,875 | 1,25 | 1,5 | 2 | 2,5 | 2,75 | 3,125 | 3,25 |
b) Với các giá trị biến x như nhau thì hàm số y=0,5x+2 luôn lớn hơn hàm số y=0,5x hai đơn vị
\(sin63^o=cos\left(90^o-63^o\right)=cos27^o\)
\(cos78^o=sin\left(90^o-78^o\right)=sin12^o\)
\(tan53^o=cot\left(90^o-53^o\right)=cot37^o\)
\(cot68^o=tan\left(90^o-68^o\right)=tan22^o\)