Tìm m để hàm số xác định với mọi x thuộc R : \(Y=\sqrt{2m\cos^2x+\left(2-m\right)\cos x+4m-1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





22 tháng 8 2021
Gọi số thú săn đc mỗi ng là a1, a2,..., a7
vì mỗi người ăn đc số thú khác nhau nên giả sử là a1<a2<ả3<...<a7
TH1:
TH2 :

DD
Đoàn Đức Hà
Giáo viên
21 tháng 8 2021
\(lim_{x\rightarrow0}\frac{7x^2}{ln\left(1+3x\right)}=lim_{x\rightarrow0}\frac{\left(7x^2\right)'}{\left(ln\left(1+3x\right)\right)'}=lim_{x\rightarrow0}\frac{14x}{\frac{3}{1+3x}}=0\)
(sử dụng quy tắc L'Hôpital)

GB
0

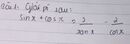


 ai đó giải giúp mình với ạ
ai đó giải giúp mình với ạ

để hàm số xác định với mọi x thuộc R thì
\(2m\cos^2x+\left(2-m\right)\cos x+4m-1\ge0\Leftrightarrow m\left(2cos^2x-cosx+4\right)\ge1-2cosx\)
mà \(2cos^2x-cosx+4>0\) nên :
\(m\ge\frac{1-2cosx}{2cos^2x-cosx+4}\)\(\Leftrightarrow\)\(m\ge max\left(\frac{1-2cosx}{2cos^2x-cosx+4}\right)=\frac{3}{7}\)
vậy điều kiện của m là : \(m\ge\frac{3}{7}\)