y= 0.24

z=0.42

t=0.12

ta có : \(\dfrac{y}{4}=\) \(\dfrac{z}{7}\) = \(\dfrac{t}{2}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{z}{7}\) = \(\dfrac{t}{2}\) = \(\dfrac{z-t}{7-2}\) = \(\dfrac{0,18}{5}\) = 0,036

\(z\) = 0,036 \(\times\) 7 = 0,252

\(t\) = 0,036 \(\times\) 2 = 0,072

\(y\) = 0,036 \(\times\) 4 = 0,144

Kết luận: \(y\) = 0,144; \(z\) = 0,252; \(t\) = 0,072

Ta thấy rằng:

\(\dfrac{1}{2}< \dfrac{2}{3}\)

\(\dfrac{3}{4}< \dfrac{4}{5}\)

...........

\(\dfrac{399}{400}< \dfrac{400}{401}\)

=> \(\dfrac{1}{2}\times\dfrac{3}{4}\times....\times\dfrac{399}{400}< \dfrac{2}{3}\times\dfrac{4}{5}\times....\times\dfrac{400}{401}\) hay \(P< \dfrac{2}{3}\times\dfrac{4}{5}\times....\times\dfrac{400}{401}\)

Ta đặt: \(B=\dfrac{2}{3}\times\dfrac{4}{5}\times....\times\dfrac{400}{401}\) 

Ta có:

\(P\times P< Q\times P\)

=> \(P^2< \dfrac{1}{2}\times\dfrac{2}{3}\times\dfrac{3}{4}\times\dfrac{4}{5}\times...\times\dfrac{399}{400}\times\dfrac{400}{401}\) 

=> \(P^2< \dfrac{1}{401}\)   mà \(\dfrac{1}{401}< \dfrac{1}{400}\) 

=> \(P^2< \dfrac{1}{400}=\left(\dfrac{1}{20}\right)^2\) 

=> \(P< \dfrac{1}{20}\) (đpcm)

\(\dfrac{r}{7}\) = \(\dfrac{s}{4}\) = \(\dfrac{t}{6}\)

Áp dụng tính chất tỉ dãy tỉ số bằng nhau ta có:

\(\dfrac{r}{7}\) = \(\dfrac{t}{6}\) = \(\dfrac{r-t}{7-6}\) = \(\dfrac{0,09}{1}\) = 0,09

\(r\) = 0,09 \(\times\) 7 = 0,63

\(t\) = 0,09 \(\times\) 6 = 0,54

\(s\) = \(\dfrac{r}{7}\) \(\times\) 4 = 0,36 

Giải bằng phương pháp giả thiết tạm em nhé:

      Giả sử số a bớt đi 10,72 đơn vị và số b bớt đi 24,2 đơn vị thì ba số bằng nhau và bằng số c

        Tổng của ba số lúc sau là:  68,7 - 10,72 - 24,2 = 33,78

         Số c là: 33,78 : 3 = 11,26 

        Số a là : 11,26 + 10,72 = 21,98

          Số b là: 11,26 + 24,2 = 35,46

         Đáp số: Số a là: 21,98

                      Số b là: 35,46 

                       Số c là: 11,26 

EM XEM hướng dẫn bài trước đã hỏi. Bài này tương tự, em tư duy một chút sẽ hiểu bài

Ta có thể giải bài toán bằng cách sử dụng phép cộng và phép trừ.

Để tìm t, ta có thể sử dụng phép cộng để tính tổng của ba số:

y + z + t = 101,3

Ta biết rằng z bé hơn t 34,4 đơn vị, hay t lớn hơn z 34,4 đơn vị. Ta có thể sử dụng phép cộng để tính t:

t = z + 34,4

Thay t vào phương trình ban đầu, ta được:

y + z + z + 34,4 = 101,3

Simplify và giải phương trình, ta có:

2z + y = 66,9

Ta biết rằng y bé hơn t 17 đơn vị, hay t lớn hơn y 17 đơn vị. Ta có thể sử dụng phép trừ để tính y:

y = t - 17

Thay t vào phương trình trên, ta được:

y = z + 34,4 - 17

Simplify và giải phương trình, ta có:

y = z + 17,4

Thay y vào phương trình 2z + y = 66,9, ta được:

2z + (z + 17,4) = 66,9

Simplify và giải phương trình, ta có:

3z = 49,5

z = 16,5

Thay z vào phương trình y = z + 17,4, ta được:

y = 33,9

Thay z và y vào phương trình t = z + 34,4, ta được:

t = 50,9

Vậy, ba số cần tìm là: y = 33,9, z = 16,5 và t = 50,9

Simplify : đơn giản hóa

Vẽ sơ đồ

t:     |---------------------------|

z:    |-------------------|34,4

y:    |----------------------|17

t = (101,3 + 34,4+17):3 = 50,9

z =  50,9 - 34,4 = 16,5

y = 50,9 - 17 = 33,9

7 \(\times\) ( 2\(x\) - 5) - 5 \(\times\) (7\(x\) - 2) + 2 \(\times\) (5\(x\) - 7) = (\(x\) - 2) - (\(x\) +4)

14\(x\) - 35 - 35\(x\) + 10 + 10\(x\) - 14 = \(x\) - 2 - \(x\) - 4

(14\(x\) - 35\(x\) + 10\(x\)) - (35 - 10+ 14)  = -6

(- 21 \(x\) + 10\(x\)) - (25 + 14) = - 6

         -11\(x\) - 39 = - 6

          -11\(x\)       = - 6 + 39

          - 11\(x\)     = 33

                \(x\) = 33 : (-11)

                \(x\) =  - 3

14x - 35 -35x + 10 + 10x - 14 = x-2-x-4

-11x -39 = -6

11x = -33

x= -3

Hiệu của tử và mẫu 2 phân số không đổi

Hiệu của tử và mẫu phân số mới:

15-7 = 8

Tử số của phân số mới:

8: (2-1) = 8

Số cần tìm là: 8-7 = 1

Khi ta cộng cả tử số và mẫu số với cùng một số thì hiệu của mẫu số và tử số lúc sau không đổi và bằng: 

                             15 - 7 = 8 

                      Theo bài ra ta có sơ đồ:

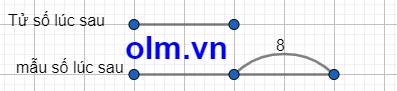
         Theo bài ra ta có sơ đồ:

              Tử số lúc sau là: 8:(2-1) = 8

               Số cần thêm vào ở cả tử số và mẫu số là:

                         8 - 7 = 1

Đáp số 1

10/18

Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có: 

Tử số là: 8:(9-5)\(\times\) 5 = 10

Mẫu số là: 10 + 8 = 18

Phân số cần tìm là \(\dfrac{10}{18}\)

Đáp số: \(\dfrac{10}{18}\)

giúp mik vớiiiiiiiiiii

Hướng dẫn: Bài toán tỉ lệ nghịch và Tổng tỉ

Cùng trên quãng đường AB thì vận tốc và thời gian tỉ lệ nghịch với nhau.

Tổng thời gian cả đi và về là: 2 giờ 45 phút = 2,75 giờ

Tỉ số thời gian khi đi và khi về là:

18: 15 = 6: 5 

Thời gian khi đi là:

2,75 : (6+5) x 6 = 1,5 (giờ)

Quãng đường AB dài:

15 x 1,5 = 22,5 (km)

Đáp số: 22,5 km