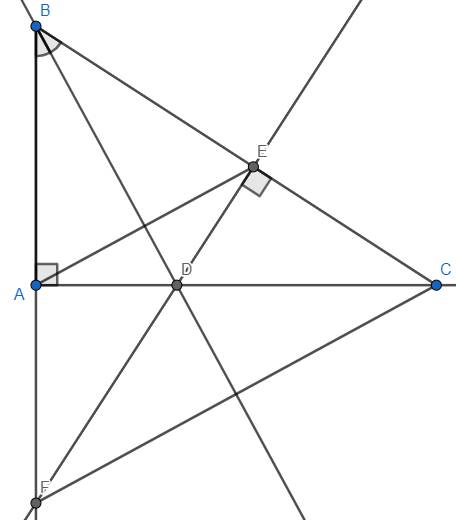
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác bed bằng tam giác BAD .
b) Tam BCF cân tại b.
c) BD là đường trung tuyến của tam giác BCF .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích hình hộp chữ nhật làm bằng bìa là:
22 x 16 x 18 = 6336 (cm3)
Đáp số: 6336cm3
Hình khối chỉ có DT toàn phần và xung quanh thôi.

c) Ta đã biết DA = DE (chứng minh trên) (1)
Trong tam giác EDC vuông tại E có DC đối diện đỉnh E
Suy ra DC là cạnh lớn nhất trong tam giác EDC
Hay DC > DE (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
ÉT Ô ÉT
Câu 3: Tìm x biết:
|x + 1| + |x + 2| + |x + 2020| = 4x
Giúp mik với!!!
Mik hứa Tick cho… Pls

TH1 : \(x< -2020\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) - ( x + 2020 ) = 4x
<=> -3x - 2023 = 4x <=> -7x = 2023 <=> x = -289
TH2 : \(-2020\le x< -2\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) + x + 2020 = 4x
<=> -x + 2017 = 4x
<=> -5x = -2017 <=> x = 2017/5 ( = 403,4 )
TH3 : \(-2\le x< -1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) + x + 2 + x + 2020 = 4x
<=> x + 2021 = 4x <=> -3x = -2021 <=> x = 2021/3
TH4 : \(x>-1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = x + 1 + x + 2 + x + 2020 = 4x
<=> 3x + 2023 = 4x
<=> -x = -2023 <=> x = 2023
Vậy...
TH1: x ≥ 0
Khi đó \(\left|x+1\right|+\left|x+2\right|+\left|x+2020\right|=x+1+x+2+x+2020\)
\(=3x+2023=4x\)
Suy ra \(4x-3x=x=2023\) (thỏa mãn điều kiện)
TH2: x < 0
Khi đó 4x < 0 hay vế phải luôn là một số âm. Tuy nhiên vế trái luôn luôn có giá trị lớn hơn 0 nên luôn là 0 hoặc là một số dương, suy ra vô lí.
Tóm lại, x = 2023.

Độ dài cạnh của hình vuông:
\(36,8:4=9,2\left(cm\right)\)
Đáp số: 9,2 cm

Gọi X là tập hợp các kết quả có thể xảy ra.
Ta có \(X=\left\{\left(1;1\right);\left(1;2\right);\left(1;3\right);...;\left(6;6\right)\right\}\). Ta thấy tập hợp trên có 36 phần tử, hoặc 36 kết quả có thể xảy ra.
a) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(4;6); (5;5); (6;4). Có 3 kết quả để biến cố trên xảy ra.
Vậy xác suất của biến cố trên là \(\dfrac{3}{36}=\dfrac{1}{12}\).
b) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(1;2); (2;1); (1;4); (2;3); (3;2); (4;1); (1;6); (2;5); (3;4); (4;3); (5;2); (6;1); (3;6); (4;5); (5;4); (6;3); (5;6); (6;5). Có 18 kết quả để biến cố trên xảy ra.
Vậy xác suất để biến cố trên xảy ra là \(\dfrac{18}{36}=\dfrac{1}{2}\).

Ta có: \(x^2+2x^2+15=3x^2+15\)
Thực hiện phép chia, ta được:
Suy ra để \(x^2+2x^2+15\) chia hết cho x + 3 thì - (9 - y)x + (15 - 3y) = 0
Hay - (9 - y)x = 15 - 3y
Khi đó \(x=\dfrac{15-3y}{-9+y}\) hay \(\left(15-3y\right)⋮\left(-9+y\right)\)
Hay \(\left[\left(15-3y\right)-3\left(-9+y\right)\right]⋮\left(-9+y\right)\)
Hay \(42⋮\left(-9+y\right)\)
Khi đó (-9 + y) ϵ Ư(42) = {1; -1; 2; -2; 3; -3; 6; -6; 7; -7; 14; -14; 21; -21; 42; -42}
Xét bảng
| -9 + y | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 | 7 | -7 | 14 | -14 | 21 | -21 | 42 | -42 |
| y | 10 | 8 | 11 | 7 | 12 | 6 | 15 | 3 | 16 | 2 | 23 | -5 | 30 | -12 | 51 | -33 |
| \(x=\dfrac{15-3y}{-9+y}\) | -15 | 9 | -9 | 3 | -7 | 1 | -5 | -1 |
-33/7 (loại) |
-9/7 (loại) | -27/7 (loại) | -15/7 (loại) | -25/7 (loại) | -17/7 (loại) | -23/7 (loại) | -19/7 (loại) |
Vậy để \(x^2+2x^2+15\) chia hết cho x + 3 thì x ϵ {-15; 9; -9; 3; -7; 1; -5; -1}
