\(A=2021-\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2021.2022}=\right)\)

\(=2021-\left(\dfrac{2-1}{1.2}+\dfrac{3-2}{2.3}+\dfrac{4-3}{3.4}+...+\dfrac{2022-2021}{2021.2022}\right)=\)

\(=2021-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\right)=\)

\(=2021-\left(1-\dfrac{1}{2022}\right)=2021-\dfrac{2021}{2022}\)

a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.

b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:

OB² = OA² + AB²

OB² = 3² + 6²

OB² = 9 + 36

OB² = 45

OB = √45 ≈ 6.71 cm

c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:

OA = 3 cm

OB = 6.71 cm

Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.

tick mik nha

a/

BC=AB-AC=4-1=3 cm

b/

CD=BC+BD

Mà BC=BD=3cm

=> CD = 3+3=6 cm

Vì điểm M nằm giữa 2 điểm O và N nên ta có:

⇔ OM + MN = ON 

Thay số : 3 + MN = 7

                       MN = 7 - 3

⇔                    MN= 4 cm.

Vì A là trung điểm của MN nên ta có:

⇔  MA = AN = MN/2

Thay số : MA = AN = 4/2 = 2cm

⇔ Điểm M nằm giữa 2 điểm O và A nên ta có:

⇔ OM + MA = OA

Thay số : 3 + 2 = OA

 ⇔ OA = 5cm.

Vậy OA = 5cm.

bn tự vẽ hình nhé

M là trung điểm của EF nên:

EM = MF = EF : 2 =  8 : 2 = 4 cm

N là trung điểm của MF nên:

NF = MN = MF : 2 = 4 : 2 = 2 cm

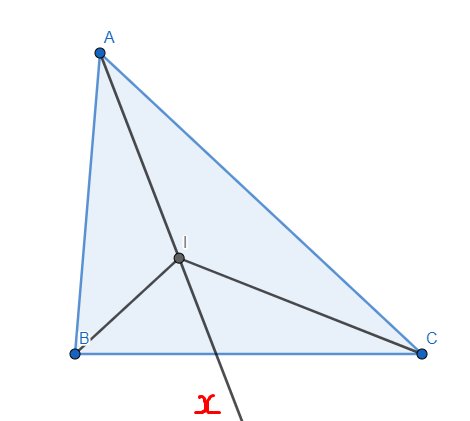
 Kẻ tia phân giác Ax của tam giác ABC. Theo tính chất góc ngoài của tam giác, dễ có \(\widehat{BIx}=\widehat{IBA}+\widehat{IAB}\) và \(\widehat{CIx}=\widehat{ICA}+\widehat{IAC}\). Cộng theo vế 2 đẳng thức trên, thu được \(\widehat{BIC}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}+\widehat{ABC}\) \(=\dfrac{180^o+\widehat{ABC}}{2}\) \(=90^o+\dfrac{\widehat{BAC}}{2}\)

 Tới đây mình cũng đã chứng minh xong câu b luôn rồi. Bạn chỉ cần thay số đo góc vào thì tính được câu a.

a) (BI và CI lần lượt là các đường phân giác của góc B và C)

Theo đề ta có:

\(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^o\)

\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=180^o-\widehat{BIC}=180^o-140^o=40^o\)

Mà \(\widehat{ABI}=\widehat{CBI}\) và \(\widehat{ACI}=\widehat{BCI}\) (vì BI và CI lần lượt là các đường phân giác của góc B và C)

Suy ra \(\widehat{ABC}+\widehat{ACB}=2\widehat{IBC}+2\widehat{ICB}=2\left(\widehat{IBC}+\widehat{ICB}\right)=2\cdot40^o=80^o\)

Từ đó 

\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)

\(\Leftrightarrow\widehat{BAC}=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)=180^o-80^o=100^o\)

a, Thời gian Trang làm bi thi thứ hai là: \(x+1\) (phút)

Thời gian Trang làm bài thi thứ ba là: (\(x+1\)).2 = 2\(x+2\)(phút)

Thời gian Trang làm bài thi thứ tư là:  2\(x+2-1\) = 2\(x+1\)

b, Thời gian Trang làm bài thi cả vòng là: 

\(x+x+1+2x+2+2x+1\) = 6\(x+\) 4 (phút)

c, Theo bài ra ta  có phương trình:

      6\(x\) + 4 = 16

      6\(x\)        = 16 - 4

      6\(x\)       = 12

        \(x\)       = 12:6

        \(x\)       = 2 (phút)

Thời gian Trang làm bài thi thứ tư là:

       2.2 + 1 = 5 (phút)

Kết luận:...

\(-22x^3-\left(-21x^3+19x^2+23^0\right)-\left(-x^3-18x^2\right)+\left(x^2-23^1\right)\)

\(=-22x^3+21x^3-19x^2-1+x^3+18x^2+x^2-23\)

\(=\left(-22x^3+21x^3+x^3\right)+\left(-19x^2+18x^2+x^2\right)+\left(-1-23\right)\)

\(=0x^3+0x^2-24\)

\(=-24\)

Vậy biểu thức trên có giá trị không phụ thuộc vào biến.

Gọi số học sinh giỏi của khối 7 là x, số học sinh khá là y

Có: \(x=\dfrac{3}{2}y\left(1\right)\)

\(\left(x+10\right)=2\left(y-6\right)\\ \Leftrightarrow x+10=2y-12\\ \Leftrightarrow x+10-2y+12=0\\ \Leftrightarrow x-2y=-22\left(2\right)\)

Thế (1) vào (2) được:

\(\dfrac{3}{2}y-2y=-22\Rightarrow y=44\)

=> x = \(\dfrac{3}{2}.44=66\)

Vậy số học sinh giỏi của khối 7 là 66 bạn.