\(3^1.3^x+5.3^x-1=162\)

\(\Leftrightarrow3^x\left(3+5\right)=163\)

\(\Leftrightarrow3^x=\dfrac{163}{8}\)

\(\Leftrightarrow x\approx2,7\)

$3^1.3^x+5.3^x-1=162$

$\iff 3^x\left(3+5\right)=163$

$\iff 3^x=\genfrac{}{}{0ex}{}{163}{8}$

$\iff x\approx 2,7$

Cho 2009 số tự nhiên liên tiếp từ 1 đến 2009 Đặt trước một số dấu "+" hoặc "-" ta được tổng A Tính giá trị không âm nhỏ nhất của tổng A

3 < 3^x < 234

3¹ < 3^x < 234

1< x < log₃234

3<3^x<234

=> x = { 2 ; 3; 4 } 

như vậy thì ta sẽ được kết quả là:  3 < 9 < 234 ; 3 < 27 < 234 ; 3 < 81 < 234 

\(x:y=2\dfrac{2}{3}=\dfrac{8}{3}\)

\(\dfrac{x}{8}=\dfrac{y}{3}\)\(\Rightarrow\dfrac{3x}{24}=\dfrac{y}{3}\)

Áp dụng ...

\(\dfrac{3x}{24}=\dfrac{y}{3}=\dfrac{3x-y}{24-3}=\dfrac{39}{21}\)

=\(\dfrac{\left(2^2\right)^3.\left(5^2\right)^5.\left(3^2\right)^3}{\left(2^3\right)^2.\left(5^3\right)^3.3^5}\)

= \(\dfrac{2^6.5^{10}.3^6}{2^6.5^9.3^5}\)

=5.3

=15

Của cháu nek-.-

ok ty gì MY

x^4=x^12

=> x1 = 8 

=> x2 = 2

=> 8^4= 2 ^12

x= 0 , 1

vì hai số này bình mấy lần cũng ra kết quả là chính nó

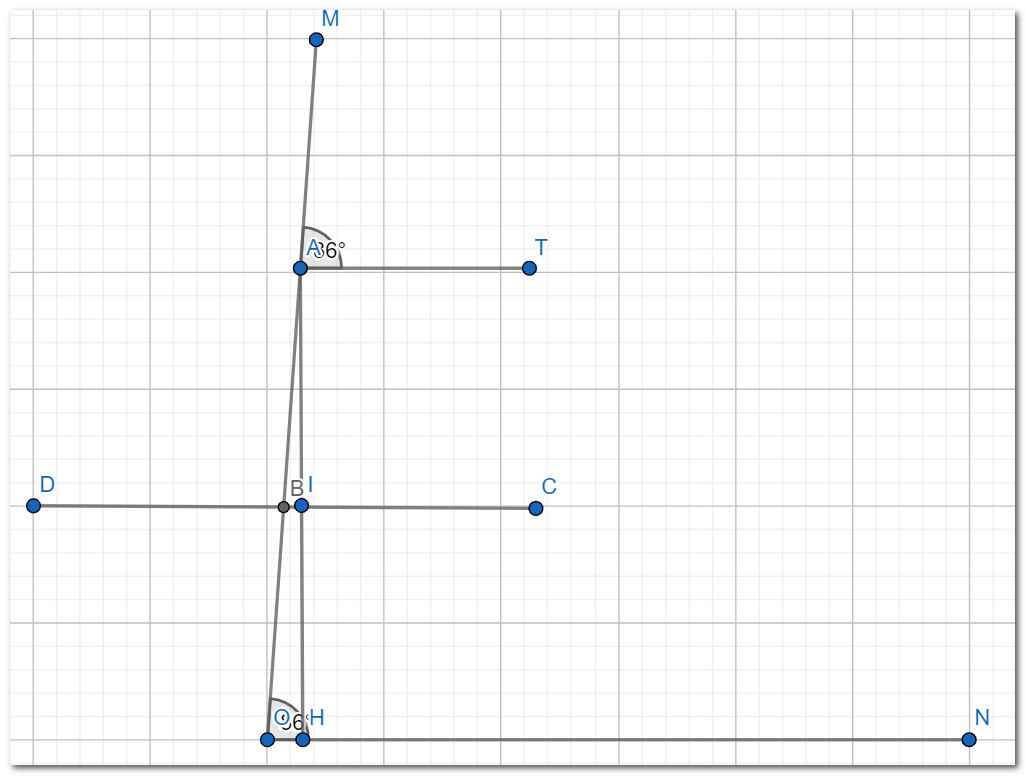
a) Ta thấy \(\widehat{mOn}=\widehat{mAt}=86^o\) mà hai góc này ở vị trí đồng vị \(\Rightarrow At//On\) (dhnb)
b) Vì \(On//At\) và \(On\perp AH\) nên \(AH\perp At\) (dhnb)(tính chất bắc cầu)
c) Vì \(AH\perp At\) nên \(\text{​​}\widehat{HAt}=90^o\)
Ta có \(\widehat{mAt}+\widehat{OAt}=\widehat{mAt}+\widehat{OAH}+\widehat{HAt}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{OAH}=180^o-\widehat{mAt}-\widehat{HAt}=180^o-86^o-90^o=4^o\)
Vậy \(\widehat{OAH}=4^o\)
d) Vì \(d\) là đường trung trực của đoạn \(AH\Rightarrow AH\perp d\Rightarrow AH\perp IB\) mà\(AH\perp At\Rightarrow At//IB\)
Mặt khác \(\widehat{OBI}\) và \(\widehat{OAt}\) là hai góc ở vị trí đồng vị \(\Rightarrow\widehat{OBI}=\widehat{OAt}\)
Vậy ta có đpcm
Lời giải của mình đây nhé bạn, chúc bạn học tốt:D