Cho tam giác ABC, đường cao AH
Chứng minh AB.AC \(\ge\) AH.BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau 7 ngày lượng gạo còn đủ cho 200 người ăn trong 5 ngày
Nếu 50 người đến thêm thì tổng số người ăn sẽ là: 250 người thì ăn trong số ngày là:
(Do số người ăn và số ngày ăn tỉ lệ nghịch nên):
\(5:\dfrac{200}{250}=\dfrac{5x4}{5}=4\) (ngày)

ĐKXĐ : \(x\ge\dfrac{1}{2}\)
Đặt \(\sqrt{2x-1}=a;\sqrt{8x+1}=b\left(a;b\ge0\right)\)
=> \(a^2=2x-1;b^2=8x+1\Rightarrow\dfrac{a^2+b^2}{10}=x\)
Lại có \((13x+1).\sqrt{2x-1}=(7x-1).\sqrt{8x+1}-4\)
\(\Leftrightarrow-\left(\sqrt{2x-1}\right)^3+15x.\sqrt{2x-1}=-\left(\sqrt{8x+1}\right)^3+15x.\sqrt{8x+1}-4\)
\(\Leftrightarrow-a^3+15ax=-b^3+15bx-4\)
\(\Leftrightarrow a^3-b^3-\dfrac{3}{2}.\left(a-b\right).\left(a^2+b^2\right)=4\)
\(\Leftrightarrow-\left(a-b\right)^3=8\)
\(\Leftrightarrow a=b-2\)
Thay vào ta được : \(\sqrt{2x-1}=\sqrt{8x+1}-2\)
\(\Leftrightarrow3x+3=2\sqrt{8x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}9x^2-14x+5=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{9}\end{matrix}\right.\)(tm ĐKXĐ)

A = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\)+ \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\)+ \(\dfrac{1}{64}\)+ \(\dfrac{1}{128}\)
A\(\times\)2 = 2 + 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + \(\dfrac{1}{64}\)
A \(\times\) 2 - A = 2 - \(\dfrac{1}{128}\)
A \(\times\)( 2-1) = \(\dfrac{255}{128}\)
A = \(\dfrac{255}{128}\)
Gọi \(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\dfrac{1}{64}+\dfrac{1}{128}\) là T
\(T=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\dfrac{1}{64}+\dfrac{1}{128}\)
\(2T=2+1+\dfrac{1}{2}+\dfrac{1}{4}+....+\dfrac{1}{64}\)
\(2T-T=\left(2+1+\dfrac{1}{2}+\dfrac{1}{4}+....+\dfrac{1}{64}\right)-\left(1+\dfrac{1}{2}+....+\dfrac{1}{64}+\dfrac{1}{128}\right)\)
\(T=2+\left(1-1\right)+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+....+\left(\dfrac{1}{64}-\dfrac{1}{64}\right)-\dfrac{1}{128}\)
\(T=2+0+0+...-\dfrac{1}{128}\)
\(T=\dfrac{256}{128}-\dfrac{1}{128}\)
\(T=\dfrac{255}{128}\)

\(=\dfrac{20}{21}x\dfrac{21}{22}x\dfrac{22}{23}x...x\dfrac{1999}{2000}\)
\(=\dfrac{20}{2000}=\dfrac{1}{100}\)
=20/21x21/22x22/23x..............x1998/1999x1999/2000
=20x21x22x23x.....................x1998x1999/21x22x23x24x...............x1999x2000
=20/2000
1/100

Xét EAF và EAC có:
+chung đường cao hạ từ e
+AF = 1/3 AC
=> S EAF= 1/3 S EAC
Xét EAC và ABC có:
+Chung đường cao hạ từ C
+AE=3/4 AB
=>S EAC =3/4 S ABC
=> S EAC= (1/3 x 3/4) S ABC = 1/4 S ABC
Tương tự
S BED =1/8 S ABC
S CDF=1/3 S ABC
=> S DEF= S ABC -S BED -S CDF
= S ABC -1/4 S ABC -1/8 S ABC -1/3 S ABC
= 7/24 S ABC
= 7/24 x 1/2 x AB x AC
= 7/24 x 1/2 x 8 x 12 =14 (cm^2)
Xét EAF và EAC có:
+chung đường cao hạ từ e
+AF = 1/3 AC
=> S EAF= 1/3 S EAC
Xét EAC và ABC có:
+Chung đường cao hạ từ C
+AE=3/4 AB
=>S EAC =3/4 S ABC
=> S EAC= (1/3 x 3/4) S ABC = 1/4 S ABC
Tương tự
S BED =1/8 S ABC
S CDF=1/3 S ABC
=> S DEF= S ABC -S BED -S CDF
= S ABC -1/4 S ABC -1/8 S ABC -1/3 S ABC
= 7/24 S ABC
= 7/24 x 1/2 x AB x AC
= 7/24 x 1/2 x 8 x 12 =14 (cm^2)

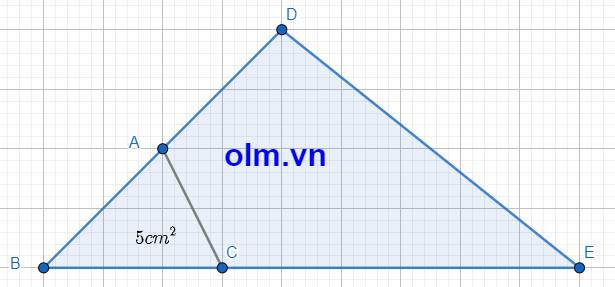
AB = AD ; BD = AB + AD ⇒ BD = AB \(\times\) 2
SBCD = SABC \(\times\) 2 (vì hai tam giác có chung đường cao hạ từ đỉnh C xuống đáy AB và BD = AB\(\times\)2) (1)
BC = \(\dfrac{1}{2}\) CE ⇒ BC \(\times\) 2 = CE
BE = BC + CE = BC + BC \(\times\) 2 = BC \(\times\) 3
SBDE = SBCD \(\times\) 3( vì hai tam giác có chung đường cao hạ từ đỉnh D xuống đáy BE và BE = BC \(\times\) 3) (2)
Kết hợp (1) và (2) ta có:
SBDE = SABC \(\times\) 2 \(\times\) 3
SBDE = 5 \(\times\) 2 \(\times\) 3 = 30( cm2)
Đáp số: 30 cm2
Đường cao tam giác ABC =h= 1/2 đường cao tam giác BDE
Cạnh BE = 3xBC
SBDE = (3xBC x2xh):2 = 6 x SABC =6x5 = 30 (cm2)

d + 15 = r + 105 ⇒ d = r + 105 - 15 ⇒ d = r + 90
Chiều dài hơn chiều rộng là: 105 - 15 = 90 (m)
Theo bài ra ta có sơ đồ:
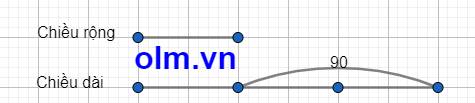
Theo sơ đồ ta có:
Chiều rộng là: 90: ( 3-1) = 45 (m)
Chiều dài là: 45 + 90 = 135 (m)
Đáp số: Chiều dài 135 m
Chiều rộng 45 m

Gọi số cần tìm là abcd
Giả sử số cần tìm đó là : 9999
Ta có : 9999 : 2021 thì được thương lớn nhất là 4 .
⇒ Thương là 4 . Số dư là 4 :
Ta có số cần tìm là :
abcd : 2021 = 4 (4)
⇒abcd = 4 x 2021 + 4 = 8088
Vậy số đó là 8088
Nếu thương lớn hơn hoặc cùng lắm là 5 ta có: 5 \(\times\) 2021 = 10105 (loại)
Nếu thương là nhỏ hơn hoặc cùng lắm là 4 thì 4\(\times\) 2021 = 8084 (thỏa mãn)
Để được số bị chia lớn nhất thì thương phải lớn nhất có thể nên thương là 4
Vì thương bằng số dư nên số dư là 4
Số bị chia cần tìm là: 4 \(\times\) 2021 + 4 = 8088
Đáp số: 8088

√4−√7−√4+√7+√7=√2(√4−√7−√4+√7+√7)√2=√8−2√7−√8+2√7+√14√2=√7−2√7+1−√7+2√7+1+√14√2=√(√7−1)2−√(√7+1)2+√14√2=∣∣√7−1∣∣−∣∣√7+1∣∣+√14√2=√7−1−√7−1+√14√2=√14−2√2=√2(√7−√2)√2=√7−√2
Lời giải:
\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}=\sqrt{\frac{8-2\sqrt{7}}{2}}-\sqrt{\frac{8+2\sqrt{7}}{2}}=\sqrt{\frac{(\sqrt{7}-1)^2}{2}}-\sqrt{\frac{(\sqrt{7}+1)^2}{2}}\)
\(=\frac{|\sqrt{7}-1|}{\sqrt{2}}-\frac{|\sqrt{7}+1|}{\sqrt{2}}=\frac{\sqrt{7}-1-(\sqrt{7}+1)}{\sqrt{2}}=\frac{-2}{\sqrt{2}}=-\sqrt{2}\)
Ta có : \(S_{ABC}=\dfrac{AH.BC}{2}\)
Kẻ đường cao từ B xuống AC tại E do đó :
\(S_{ABC}=\dfrac{BE.AC}{2}\)
mà \(BE< AB\) ( AB là cạnh huyền trong tam giác ABE )
Do đó :
\(\dfrac{AB.AC}{2}\ge\dfrac{BE.AC}{2}=\dfrac{AH.BC}{2}\)
\(\Rightarrow AB.AC\ge AH.BC\left(đpcm\right)\)
Dấu bằng xảy ra khi và chỉ khi : BE trùng với AB
\(\Leftrightarrow\Delta ABC\) vuông tại A .