(3,5 điểm)
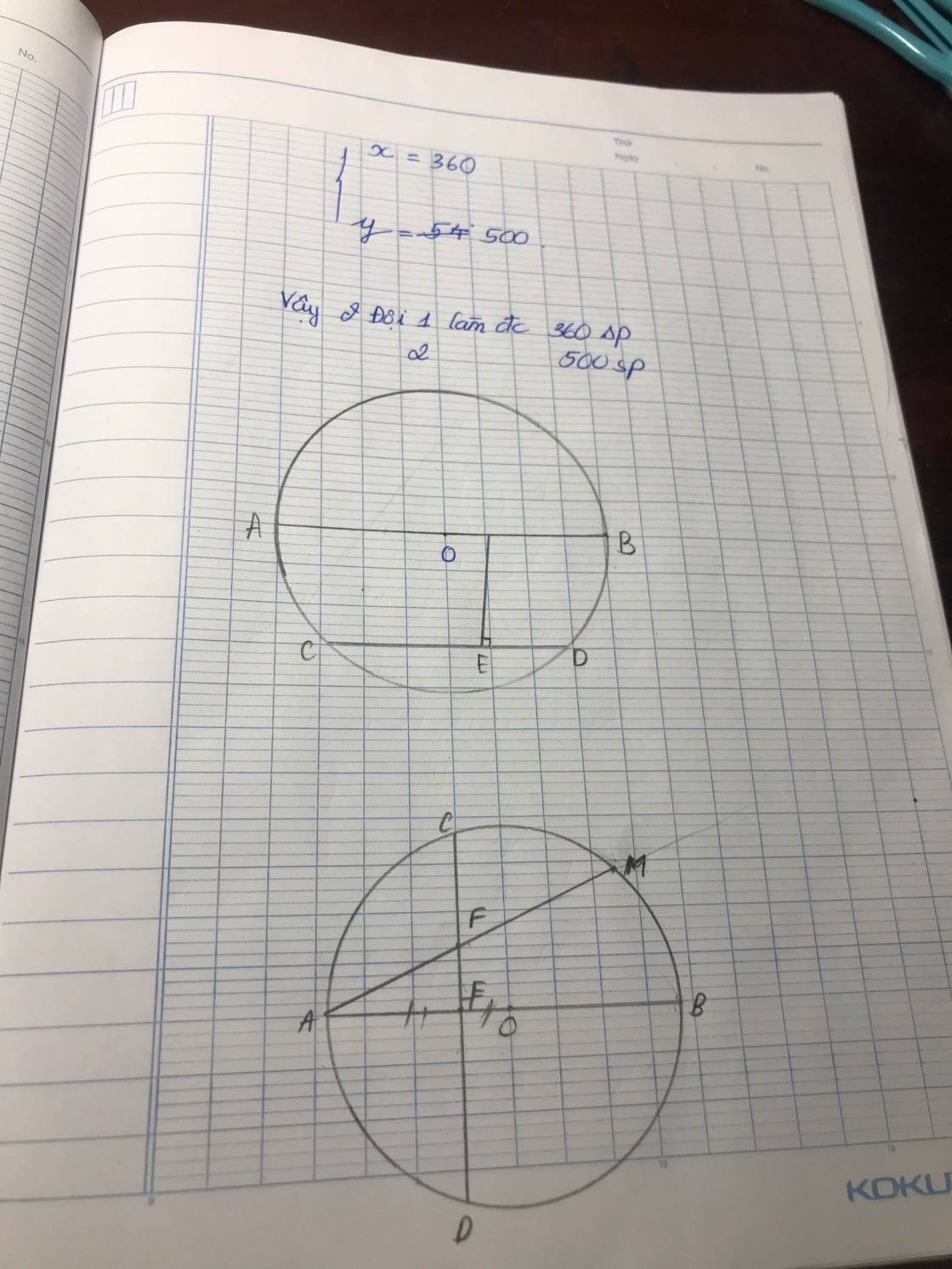
Cho đường tròn $(O)$ đường kính $BC$. Trên đường tròn $(O)$ lấy điểm $A$ sao cho $AB<AC$. Trên $OC$ lấy điểm $M$ sao cho $M$ nằm giữa $O$ và $C$. Qua $M$ kẻ đường thẳng vuông góc với $OC$ cắt tia đối của tia $AB$ tại $N$, cắt $AC$ tại $F$. Đường thẳng $NM$ cắt đường tròn $(O)$ tại $F$ và $K$ ($F$ nằm giữa $E$ và $N$).
a) Chứng minh bốn điểm $A$, $B$, $M$, $E$ cùng thuộc một đường tròn, bốn điểm $N$, $A$, $M$, $C$ cùng thuộc một đường tròn.
b) Vẽ tiếp tuyến tại $A$ của đường tròn $(O)$ cắt $MN$ tại $H$. Chứng minh rằng tam giác $AHE$ là tam giác cân.
c) Gọi giao điểm thứ hai của $NC$ với đường tròn $(O)$ là $D$. Chứng minh $HD$ là tiếp tuyến của đường tròn $(O)$.