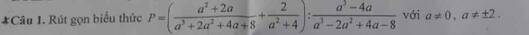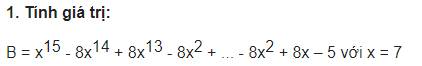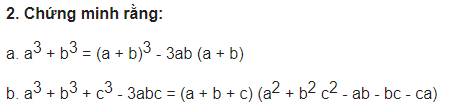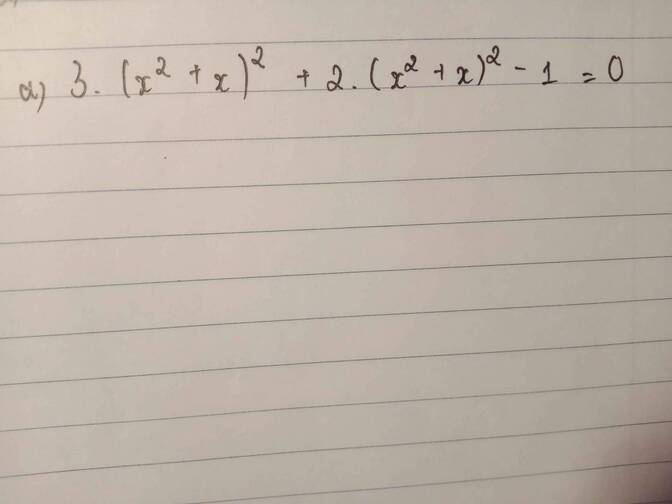khó thế

\(P=\left(\dfrac{a^2+2a}{a^3+2a^3+4a+8}+\dfrac{2}{a^2+4}\right)\div\dfrac{a^3-4a}{a^3-2a^2+4a-8}\)

\(=\left[\dfrac{a\left(a+2\right)}{\left(a+2\right)\left(a^2+4\right)}+\dfrac{2}{a^2+4}\right].\dfrac{\left(a-2\right)\left(a^2+4\right)}{a\left(a^2-4\right)}\)

\(=\dfrac{a+2}{a^2+4}.\dfrac{\left(a-2\right)\left(a^2+4\right)}{a.\left(a-2\right)\left(a+2\right)}=\dfrac{1}{a}\)

\(\dfrac{x^2+1}{3x-13}\)<0

\(\Leftrightarrow\)x\(^2\)+1<0

\(\Leftrightarrow\)x\(^2\)<-1 (vô lí)

Vậy bất phương trình vô nghiệm

\(\dfrac{x^2+1}{3x-13}\)<0 ( x khác 13/3)

mà x²+1>0

=> 3x-13 <0

=> x<13/3

nhanh hộ mik ạ

mik đang cần gấp ạ

Gọi số học sinh giỏi năm 2018-2019 là \(x\)(học sinh) \(x\inℕ^∗\).

Số học sinh giỏi năm 2019-2020 là \(\left(1+15\%\right)x=1,15x\) (học sinh) 

Vì tổng số học sinh giỏi hai năm là \(473\) nên ta có phương trình: 

\(x+1,15x=473\)

\(\Leftrightarrow x=220\) (thỏa mãn) 

Vậy số học sinh giỏi năm 2019-2020 là \(1,15.220=253\) học sinh. 

Gọi số học sinh giỏi năm 2018-2019 là $x$(học sinh) $x\in N^{\ast }$.

Số học sinh giỏi năm 2019-2020 là $\left(1+15\%\right)x=1,15x$ (học sinh) 

Vì tổng số học sinh giỏi hai năm là $473$ nên ta có phương trình: 

$x+1,15x=473$

$\iff x=220$ (thỏa mãn) 

Vậy số học sinh giỏi năm 2019-2020 là $1,15.220=253$ học sinh. 

Giải bằng cách lập PT .Trường có số hsg năm 2019-2020 tăng 15% so với năm 2018.Biết sô hs của 2 năm là 473 .Tính số hsg của năm 2019-2020

ta có m>n

Giúp mìnk vớiiii 

`Answer:`

1.

Ta có: `8=7+1=x+1`

\(B=x^{15}-8x^{14}+8x^{13}-...-8x^2+8x-5\)

\(=x^{15}-\left(x+1\right).x^{14}+\left(x+1\right).x^{13}-...-\left(x+1\right).x^2+\left(x+1\right).x-5\)

\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-...-x^3-x^2+x^2+x-5\)

\(=x-5\)

\(=7-5=2\)

2.

a. \(VP=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2\)

\(=\left(a^3+b^3\right)+\left(3a^2b-3a^2b\right)+\left(3ab^2-3ab^2\right)\)

\(=a^3+b^3=VT\)

b. \(VT=a^3+b^3+c^3-3abc\)

\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)

\(=\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right).c+c^2\right]-3ab\left(a+b+c\right)\)

\(=\left(a+b+c\right)\left(a^2+b^2+c^2+2ab-ac-bc-3ab\right)\)

\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=VP\)

Giúp mk nka :)

\(3\left(x^2+x\right)^2+2\left(x^2+x\right)^2-1=0\)

Đặt \(\left(x^2+x\right)^2=a\)

pt⇔ \(3a+2a-1=0\)

\(\Leftrightarrow5a=1\)

\(\Leftrightarrow a=\dfrac{1}{5}\)

\(\Rightarrow\left(x^2+x\right)^2=\dfrac{1}{5}\)

\(\Rightarrow\left[{}\begin{matrix}x^2+x=\dfrac{1}{\sqrt{5}}\\x^2+x=-\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)

Đến đây chuyển vế dùng delta là được