67+59= +60
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2. So sánh: A = \(\dfrac{1}{41}\) + \(\dfrac{1}{42}\) + \(\dfrac{1}{43}\) + \(\dfrac{1}{44}\)+...+ \(\dfrac{1}{80}\) và B = \(\dfrac{7}{12}\)
\(\dfrac{1}{41}>\dfrac{1}{42}>\dfrac{1}{43}>...>\dfrac{1}{60}\)
Xét mẫu số các phân số trên lần lượt là các số thuộc dãy số sau:
41; 42; 43;...;60
Dãy số trên là dãy số cách đều với khoảng cách là: 42 - 41 =1
Số số hạng của dãy số trên là: (60 - 41):1 + 1 = 20
⇒ \(\dfrac{1}{41}\) + \(\dfrac{1}{42}\)+...+ \(\dfrac{1}{60}\) > \(\dfrac{1}{60}\) \(\times\) 20 = \(\dfrac{1}{3}\) (1)
Chứng minh tương tự ta cũng có:
\(\dfrac{1}{61}+\dfrac{1}{62}+...+\dfrac{1}{80}\) > \(\dfrac{1}{80}\) \(\times\) 20 = \(\dfrac{1}{4}\) (2)
Kết hợp(1) và (2) ta có:
A = \(\dfrac{1}{41}+\dfrac{1}{42}+\dfrac{1}{43}+\dfrac{1}{44}+...+\dfrac{1}{80}\) > \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\) = \(\dfrac{7}{12}\)
Vậy A > B

Ta có: SBC = T x SC
=> SBC = 67 x SC
Lại có: SBC + 16 = 69 x SC
=> 69xSC - 67xSC = 2xSC =(SBC+16) - SBC = 16
=> SC = 8
=> SBC = 67 x 8 = 536
Vậy phép chia là 536 : 8 = 67

Đổi 1 giờ 46 phút thành giờ
Thời gian Nam đi quãng đường là:
(giờ)
Thời gian Nam đi quãng đường là:
(giờ)
Tổng thời gian đi quãng đường là:
(km)
Quãng đường AB ngắn hơn quãng đường BC là bao nhiêu thì mới đủ dữ liệu em nhé

Có a:b:c=2:4:5
\(\Rightarrow\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}\) \(=\dfrac{a+b-c}{2+4-5}=3\)
\(\dfrac{a}{2}=3\) \(\Rightarrow a=6\)
\(\dfrac{b}{4}=3\) \(\Rightarrow b=12\)
\(\dfrac{c}{5}=3\) \(\Rightarrow c=15\)
Ta có : \(\dfrac{a}{2}\) = \(\dfrac{b}{4}\) = \(\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau: ta có:
\(\dfrac{a}{2}\) = \(\dfrac{b}{4}\) = \(\dfrac{c}{5}\) = \(\dfrac{a+b-c}{2+4-5}\) = \(\dfrac{3}{1}\) = 3
\(a\) = 3 \(\times\) 2 = 6
\(b\) = 3 \(\times\) 4 = 12
\(c\) = 3 \(\times\) 5 = 15
Kết luận: \(a\) = 6; \(b\) = 12; \(c\) = 15

\(3^{n+2}+3^{n+1}-3^n=891\)
\(3^n\times3^2+3^n\times3-3^n=891\)
\(3^n\times\left(9+3-1\right)=891\)
\(3^n\times11=891\)
\(3^n=891\div11\)
\(3^n=81\)
\(3^n=3^4\)
\(n=4\)

Ta có \(p=x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}=2\). Ta đi tìm GTNN của \(B=p+\dfrac{1}{p}\).
Do \(B=\dfrac{p}{4}+\dfrac{1}{p}+\dfrac{3p}{4}\) \(\ge2\sqrt{\dfrac{p}{4}.\dfrac{1}{p}}+\dfrac{3.2}{4}\) \(=\dfrac{5}{2}\). ĐTXR \(\Leftrightarrow\left\{{}\begin{matrix}x=y\\p=2\end{matrix}\right.\) \(\Leftrightarrow x=y=1\).
Vậy GTNN của B là \(\dfrac{5}{2}\) khi \(x=y=1\)

Dãy số trên là dãy số cách đều với khoảng cách là:
93 109 - 93 009 = 100
Vậy số tiếp theo cần điền vào chỗ còn thiếu là:
93 109 + 100 = 93 209
Đáp số: 93 209
Dãy số trên là dãy số cách đều với khoảng cách là:
93 109 - 93 009 = 100
Vậy số tiếp theo cần điền vào chỗ còn thiếu là:
93 109 + 100 = 93 209
Đáp số: 93 209

Số chân chó là:
\(128\times4=512\left(chan\right)\)
Số chân mèo:
\(128\times4=512\left(chan\right)\)
Tổng chân chó và chân mèo:
\(512+512=1024\left(chan\right)\)
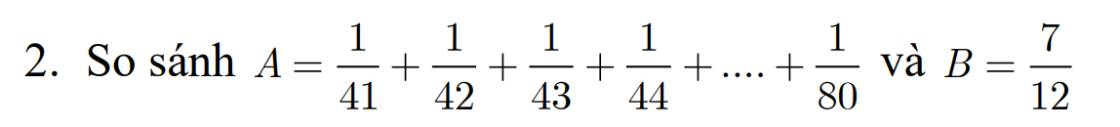
67 + 59 = ...+ 60
126 = ...+60
126 - 60 = ...
66 = ...
Kết luận số thích hợp điền vào chỗ ... là 66
67 + 59 = ...+ 60
126 = ...+60
126 - 60 = ...
66 = ...
ui dời ơi dễ vãi nồi