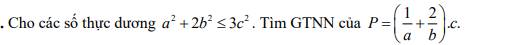a, Xét tam giác ABC và tam giác HAC có 

^BCA _ chung 

^BAC = ^AHC = 90⁰

Vậy tam giác ABC ~ tam giác HAC (g.g) 

\(\dfrac{AB}{AH}=\dfrac{AC}{HC}\Rightarrow AB.HC=AC.AH\)

b, Theo định lí Pytago tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=10cm\)

Ta có \(\dfrac{AB}{AH}=\dfrac{BC}{AC}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{24}{5}cm\)

\(\Rightarrow CH=\dfrac{AC.AH}{AB}=\dfrac{\dfrac{8.24}{5}}{6}=\dfrac{32}{5}cm\)

\(\left(2x+1\right)\left(3x-2-5x+6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)

a) \(A=x^2-6x+9-9y^2\)

\(=\left(x-3\right)^2-\left(3y\right)^2\)

\(=\left(x-3-3y\right)\left(x-3+3y\right)\)

b) \(B=x^3-3x^2+3x-1+2\left(x^2-1\right)\)

\(=\left(x-1\right)^3+\left(2x+2\right)\left(x-1\right)\)

\(=\left(x-1\right)\left[\left(x-1\right)^2+2x+2\right]\)

\(=\left(x-1\right).\left(x^2+3\right)\)

a, \(A=\left(x-3\right)^2-9y^2=\left(x-3-3y\right)\left(x-3+3y\right)\)

b, \(B=\left(x-1\right)^3+2\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left[\left(x-1\right)^2+2\left(x+1\right)\right]\)

\(=\left(x-1\right)\left(x^2-2x+1+2x+2\right)=\left(x-1\right)\left(x^2+3\right)\)

\(x^3+2x^2+x\)

\(=x\left(x^2+2x+1\right)\)

\(=x\left(x+1\right)^2\)

\(x\left(x^2+2x+1\right)=x\left(x+1\right)^2\)

`3x-6` không âm tức là `>= 0`

`=>3x-6 >= 0`

`<=>3x >= 6`

`<=>x >= 2`

Vậy `S={x|x >= 2}`

ai trả lời hộ mik với

gọi số sản phẩm tổ phải sản xuất theo kế hoạch là : x (x ϵ N*)

→số sản phảm thực tế tổ làm đc là : x+15

theo thực tế thì 1 ngày tổ đó làm đc: 60+5=65(sản phẩm)

ta có, theo thực tế thì tổ đó hoàn thành sản phẩm trước 2 ngày:

→ ta có phương trình

\(\dfrac{x}{60}\)-\(\dfrac{x+15}{65}\)=2

giải hệ phương trình, ta được x=1740(thỏa mãn)

a, Xét tam giác ABC và tam giác HBA có 

^ABC _ chung 

^BAC = ^BHA = 90⁰

Vậy tam giác ABC ~ tam giác HBA (g.g) 

b, Theo định lí Pytago tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=10cm\)

c, Chu vi tam giác ABC là 

10 + 6 + 8 = 24 cm 

d, Ta có \(\dfrac{AB}{HB}=\dfrac{BC}{AB}\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)

Lại có \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\Rightarrow AH=\dfrac{AC.AB}{BC}=\dfrac{48}{10}=\dfrac{24}{5}cm\)

Áp dụng bất đẳng thức Cauchy Schwartz, ta được:

\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1^2}{a}+\dfrac{2^2}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\)

Áp dụng bất đẳng thức Cauchy Schwartz, ta được:

\(\left(a+2b\right)^2=\left(a.1+\sqrt{2}.\sqrt{2}b\right)^2\le\left(a^2+2b^2\right).3\)

\(\Rightarrow a+2b\le\sqrt{3\left(a^2+2b^2\right)}\le\sqrt{9c^2}=3c\)

\(\Rightarrow\dfrac{1}{a}+\dfrac{2}{b}\ge\dfrac{9}{3c}=\dfrac{3}{c}\)

\(\Rightarrow P\ge\dfrac{3}{c}.c=3\)

Dấu "=" xảy ra khi \(a=b=c=1\)