Tỉ số bán kính hình tròn thứ nhất và hình tròn thứ hai là 3/4 thì tỉ số diện tích của hình tròn thứ nhất và hình tròn thứ hai là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta đặt:
\(A=1^n+2^n+3^n+4^n\)
Nếu n là số lẻ thì \(1^n+4^n⋮5;2^n+3^n⋮5\)
Nên \(A⋮5\)
Nếu n = 4K + 2 \(\left(k\in N\right)\) thì
\(A=1+2^{4K+2}+3^{4K+2}+4^{4K+2}=\left(1+4^{2K+1}\right)+\left(9^{2K+1}+16^{2K+1}\right)⋮5\)
Nếu n = 4K \(\left(K\in N\right)\) thì
\(A=1+2^{4K}+3^{4K}+4^{4K}=1+16^K+81^K+256^K\)
Có chữ số tận cùng là 4, không chia hết cho 5
\(\Rightarrow1^n+2^n+3^n+4^n⋮5\) khi \(n⋮̸4\left(đpcm\right)\)

\(\dfrac{1}{3\times7}\) + \(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\) = \(\dfrac{49}{597}\)
(\(\dfrac{1}{3\times7}\)+ \(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\))\(\times\)4 = \(\dfrac{49}{597}\)\(\times\) 4
\(\dfrac{4}{3\times7}\)+\(\dfrac{4}{7\times11}\)+\(\dfrac{4}{11\times15}\)+...+\(\dfrac{4}{a\times\left(a+4\right)}\) = \(\dfrac{196}{597}\)
\(\dfrac{1}{3}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) + \(\dfrac{1}{11}\)- \(\dfrac{1}{15}\)+...+ \(\dfrac{1}{a}-\dfrac{1}{a+4}\) = \(\dfrac{196}{597}\)
\(\dfrac{1}{3}\) - \(\dfrac{1}{a+4}\) = \(\dfrac{196}{597}\)
\(\dfrac{1}{a+4}\) =\(\dfrac{1}{3}-\) \(\dfrac{196}{597}\)
\(\dfrac{1}{a+4}\) = \(\dfrac{1}{199}\)
\(a\) + 4 = 199
\(a\) = 199 - 4
\(a\) = 195

X = {5; 7; 9; 11; 13;...;83}
Xét dãy số: 5; 7; 9;11; 13;...; 83
Dãy số trên là dãy số cách đều có khoảng cách là: 7 - 5 = 2
Phần tử thứ 11 của tập hợp X chính là số hạng thứ 11 của dãy số trên
Áp dụng công thức tính số thứ n của dãy số cách đều:
Stn = số đầu + khoảng cách \(\times\)(n-1)
Số thứ 11 của dãy số trên là: 5 + 2 \(\times\) ( 11 - 1) = 25
Kết luận:
Phần tử đứng thứ 11 tính từ trái qua phải của tập hợp X khi các phần tử của tập hợp X được sắp xếp theo thứ tự từ bé đến lớn là: 25

Gỉa thiết tạm biết hiệu em nhé:
Nếu coi càng cua là chân cua thì mỗi con cua có số chân là:
8 + 2 = 10 chân
Giả sử tất cả đều là cua thì thì tổng số chân là:
10 \(\times\) 200 = 2000 (chân)
Số chân cua nhiều hơn số chân ếch là 2000 chân
So với đề bài thì thừa ra số chân là: 2000 - 180 = 1820 (chân)
Cứ thay một con cua bằng một con ếch thì số chân giảm là:
10 + 4 = 14 (chân)
Số con ếch là: 1820: 14 = 130 (con)
Số cua là: 200 - 130 = 70 (con)
Đáp số: Cua 70 con; ếch 130 con
Thử lại kết quả ta có: Tổng số cua và ếch là: 70 + 130 = 200 (ok)
Số chân cua nhiều hơn số chân ếch là:
70 \(\times\) 10 - 130 \(\times\) 4 = 180 (ok) Vậy kết quả bài toán là đúng em nhé

a) \(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2009.2010}\)
\(A=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2009}-\dfrac{1}{2010}\)
\(A=\dfrac{1}{1}-\dfrac{1}{2010}\)
\(A=\dfrac{2009}{2010}\)
b) \(B=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{2009.2011}\)
\(B=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\)
\(B=1-\dfrac{1}{2011}\)
\(B=\dfrac{2010}{2011}\)
b) B= \(\dfrac{2}{1.3}\)+ \(\dfrac{2}{3.5}\)+ ... + \(\dfrac{2}{2010.2012}\)
B= 1 - \(\dfrac{1}{3}\)+ \(\dfrac{1}{3}\) - \(\dfrac{1}{5}\)+...+ \(\dfrac{1}{2010}\) - \(\dfrac{1}{2012}\)
B= 1 - \(\dfrac{1}{2012}\)
B= \(\dfrac{2011}{2012}\)

\(\dfrac{1}{3\times7}+\dfrac{1}{7\times11}+\dfrac{1}{11\times15}+...+\dfrac{1}{a\times\left(a+4\right)}=\dfrac{50}{609}\)
\(\dfrac{1}{4}\times\left(\dfrac{4}{3\times7}+\dfrac{4}{7\times11}+...+\dfrac{4}{a\times\left(a+4\right)}\right)=\dfrac{50}{609}\)
\(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{a}-\dfrac{1}{a\times4}=\dfrac{50}{609}\div\dfrac{1}{4}\)
\(\dfrac{1}{3}-\dfrac{1}{a\times4}=\dfrac{200}{609}\)
\(\dfrac{1}{a\times4}=\dfrac{1}{3}-\dfrac{200}{609}\)
\(\dfrac{1}{a\times4}=\dfrac{1}{203}\)
\(a\times4=203\)
\(a=\dfrac{203}{4}\)
\(\dfrac{1}{3\times7}\)+\(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\) = \(\dfrac{50}{609}\)
4\(\times\)( \(\dfrac{1}{3\times7}\) +\(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\)) = \(\dfrac{50}{609}\) \(\times\)4
\(\dfrac{4}{3\times7}\)+ \(\dfrac{4}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{4}{a\times\left(a+4\right)}\) = \(\dfrac{50}{609}\) \(\times\) 4
\(\dfrac{1}{3}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) + \(\dfrac{1}{11}\)-\(\dfrac{1}{15}\)+...+\(\dfrac{1}{a}\)-\(\dfrac{1}{a+4}\) = \(\dfrac{200}{609}\)
\(\dfrac{1}{3}\) - \(\dfrac{1}{a+4}\) = \(\dfrac{200}{609}\)
\(\dfrac{1}{a+4}\) = \(\dfrac{1}{3}\) - \(\dfrac{200}{609}\)
\(\dfrac{1}{a+4}\) = \(\dfrac{1}{203}\)
a + 4 = 203
\(a\) = 203 - 4
\(a\) = 199
Đáp số: \(a\) = 199

Dùng phương pháp giải ngược của tiểu học
Nếu lần thứ ba bà không bán thêm 1 quả thì số cam còn lại sau ba lần bán là:
3 + 1 = 4 (quả)
4 quả cam ứng với số phần là:
1-\(\dfrac{2}{3}\)=\(\dfrac{1}{3}\)(số cam còn lại sau lần bán thứ hai)
Số cam còn lại sau lần bán thứ hai là:
4 : \(\dfrac{1}{3}\) = 12 (quả)
Nếu lần thứ hai bà không bán thêm 2 quả thì số cam còn lại là:
12 + 2 = 14 (quả)
14 quả ứng với phân số là:
1 - \(\dfrac{3}{4}\) = \(\dfrac{1}{4}\)(số cam còn lại sau lần bán thứ nhất)
Số cam còn lại sau lần bán thứ nhất là:
14 : \(\dfrac{1}{4}\) = 56 (quả)
Nếu lần thứ nhất bà không bán thêm 1 quả thì số cam còn lại là:
56 + 1 = 57 (quả)
57 quả ứng với phân số là:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)(số cam)
Ban đầu bà có tất cả số cam là:
57 : \(\dfrac{1}{2}\) = 114 (quả)
Đáp số: 114 quả
Đáp án:
quả
Phân số chỉ số cam còn lại sau lần bán thứ là :
(số cam)
Phân số chỉ số cam bán lần là :
(số cam)
Phân số chỉ quả cam là :
(số cam)
Lúc đầu bà có số quả cam là :
(quả)
Đáp số : quả
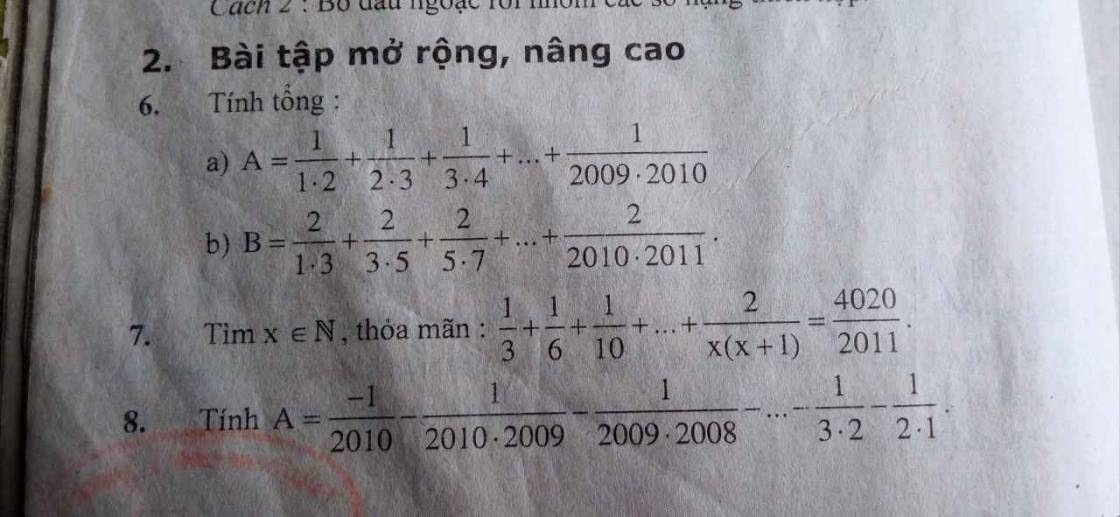
Tỉ số bán kính hình tròn thứ nhất và hình tròn thứ hai là: \(\dfrac{3}{4}\)
Thì tỉ số diện tích hình tròn thứ nhất và hình tròn thứ hai là
\(\dfrac{3}{4}\) \(\times\) \(\dfrac{3}{4}\) = \(\dfrac{9}{16}\)
Đáp số: \(\dfrac{9}{16}\)