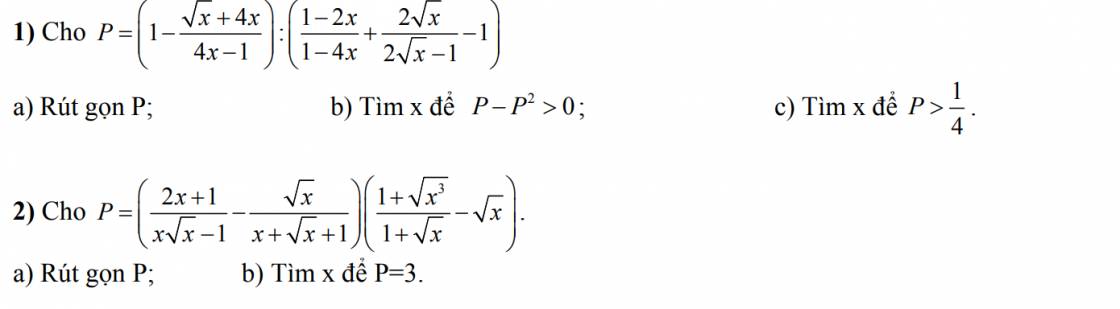\(a^3-x-x^3+a=0\)

\(\Leftrightarrow a^3-x^3+\left(a-x\right)=0\)

\(\Leftrightarrow\left(a-x\right)\left(a^2+ax+x^2\right)+\left(a-x\right)=0\)

\(\Leftrightarrow\left(a-x\right)\left(a^2+ax+x^2+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=x\\a^2+ax+x^2+1=0\left(2\right)\end{matrix}\right.\)

\(\left(2\right)\Leftrightarrow a^2+ax+x^2+1=0\)

Ta có:\(a^2+ax+x^2+1=a^2+2.a.\dfrac{1}{2}x+\dfrac{1}{4}x^2+\dfrac{3}{4}y^2+1\)

                                     \(=\left(a+\dfrac{1}{2}x\right)^2+\dfrac{3}{4}y^2+1>0\)

\(\Rightarrow\left(2\right)\) vô lý

Vậy \(a=x\)

\(B=x^{2020}-2018x^{2019}-2018x^{2018}-...-2018x+1\)

\(=x^{2020}-2019x^{2019}+x^{2019}-2019x^{2018}+x^{2018}-2019x^{2017}+...+x^2-2019x+x+1\)

\(=x^{2019}\left(x-2019\right)+x^{2018}\left(x-2019\right)+x^{2017}\left(x-2019\right)+...+x\left(x-2019\right)+x+1\)Thay \(x=2019\) vào B ta có:

\(B=2019^{2019}\left(2019-2019\right)+2019^{2018}\left(2019-2019\right)+2019^{2017}\left(2019-2019\right)+...+2019\left(2019-2019\right)+2019+1\)

\(=2019+1=2020\)

.2,đk x >= 0 ; x khác 1 

 \(P=\left(\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{x\sqrt{x}-1}\right)\left(\dfrac{1+x\sqrt{x}-\sqrt{x}-x}{\sqrt{x}+1}\right)\)

\(=\dfrac{x+\sqrt{x}+1}{x\sqrt{x}-1}\left(\dfrac{x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\right)\)

\(=\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)}=\sqrt{x}-1\)

Ta có \(\sqrt{x}-1=3\Leftrightarrow x=16\left(tm\right)\)

phương pháp 

giả sử tồn tại n để \(\dfrac{n+20}{n+90}\) là bình phương của một số hữu tỉ  thì sẽ tồn tại một phân số \(\dfrac{a}{b}\) thỏa mãn

\(\dfrac{n+20}{n+90}\) =  ( \(\dfrac{a}{b}\))²

⇔  b² - a² = 70 ⇔ (b-a)(b+a) = 70 = 10 . 7 = 14 x 5 = 35 x 2

với a,b là các số tự nhiên thì \(\left\{{}\begin{matrix}b-a=7\\a+b=10\end{matrix}\right.\) vô nghiệm tương tự

các trường hợp còn lại cũng vô nghiệm vậy ko có giá trị nào của n thỏa mãn đề bài  

đây là phương pháp phản chứng nhé bạn

A = m² + n² = (m+n)² - 2mn = 10² - 2 . 5 = 90

B = m³n + m.n³ = mn (m² +n²) = 5 . 90 = 450

C = 1/m + 1/n = \(\dfrac{m+n}{mn}\) = \(\dfrac{10}{5}\) = 2

D = m - n =   \(\sqrt{m^{2^{ }}-2mn+n^2}\) = \(\sqrt{90-5.2}\)= \(\sqrt{80}\) =4\(\sqrt{5}\)

cảm ơn

Bài 1:

\(a-c=m^2+n^2-2mn=\left(m-n\right)^2>0\)

\(\Rightarrow a>c\)

\(a-b=m^2+n^2-m^2+n^2=2n^2>0\)

\(\Rightarrow a>b\)

\(a-\left(b+c\right)=m^2+n^2-\left(m^2-n^2+2mn\right)=2n^2-2mn=2n\left(n-m\right)< 0\)

\(\Rightarrow b+c>a\) mà \(a>b,a>c\)

\(\Rightarrow a,b,c\) là độ dài 3 cạnh của 1 tam giác.

Ta có: \(b^2+c^2=\left(m^2-n^2\right)+4m^2n^2=m^4-2m^2n^2+n^4+4m^2n^2=m^4+2m^2n^2+n^4=\left(m^2+n^2\right)^2\)

\(a^2=\left(m^2+n^2\right)^2\)

\(\Rightarrow a^2=b^2+c^2\)

\(\Rightarrow a,b,c\) là độ dài 3 cạnh của tam giác vuông (định lí Py-ta-go đảo).

Bài 2:

a) \(a^2-b^2-c^2+2bc=a^2-\left(b-c\right)^2=\left(a-b+c\right)\left(a+b-c\right)=\left(2m-2b\right)\left(2m-2c\right)=4\left(m-b\right)\left(m-c\right)\left(đpcm\right)\)

a, Theo định lí Pytago tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=10cm\)

Vì AD là phân giác \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\Rightarrow\dfrac{CD}{AC}=\dfrac{BD}{AB}\)

Theo tc dãy tỉ số bằng nhau 

\(\dfrac{CD}{AC}=\dfrac{BD}{AB}=\dfrac{BC}{AC+AB}=\dfrac{10}{14}=\dfrac{5}{7}\Rightarrow CD=\dfrac{40}{7}cm;BD=\dfrac{30}{7}cm\)

Xét tam giác ABH và tam giác CBA có 

^AHB = ^BAC = 90⁰

^ABH _ chung 

Vậy tam giác ABH ~ tam giác CBA (g.g)

\(\dfrac{AB}{BC}=\dfrac{BH}{AB}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)

-> DH = BD - BH = \(\dfrac{30}{7}-\dfrac{18}{5}=\dfrac{150-136}{35}=\dfrac{14}{35}=\dfrac{2}{5}\)cm 

b, \(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}cm\)

Vì HM vuông AB; HN vuông AC ; BA vuông AC nên tg AMHN là hcn 

=> AH = MN = 24/5 cm 

c, Xét tam giác AHM và tam giác ABH có 

^HAM _ chung ; ^AMH = ^AHB = 90⁰

Vậy tam giác AHM ~ tam giác ABH (g.g) 

\(\dfrac{AH}{AB}=\dfrac{AM}{AH}\Rightarrow AH^2=AM.AB\)

tương tự tam giác AHN ~ tam giác ACH (g.g)

\(\dfrac{AH}{AC}=\dfrac{AN}{AH}\Rightarrow AH^2=AN.AC\)

=> AM . AB = AN . AC 

Câu c là AM. AB=AN. AC nha mn giúp mik vs 

\(x^3-x^2-x^2+x=0\Leftrightarrow x^3-2x^2+x=0\)

\(\Leftrightarrow x\left(x^2-2x+1\right)=0\Leftrightarrow x\left(x-1\right)^2=0\Leftrightarrow x=0;x=1\)