Tính hợp lí (nếu có thể)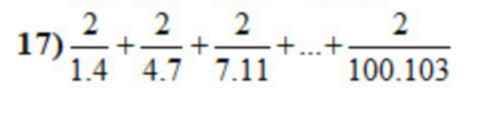
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BG
Nửa chu vi của thửa ruộng là:
240:2=120 (m)
chiều dài của thửa ruộng là:
(120 + 20) :2= 70(m)
chiều rộng thửa ruộng là:
120 - 70 = 50 (m)
Diện tích thửa ruộng đó là :
70 x 50= 350(m2)
Đáp số : 350 m2
Nữa chu vi là 240:2 =120 (m)
Chiều dài là : ( 120 + 20 ) : 2= 70 (m)
Chiều rộng là: 120 - 70 = 50 (m)
Diện tích là: 70 x 50 = 350 (m2)
Đáp số: 350 m2

Cứ 1 điểm sẽ tạo với 3 - 1 điểm còn lại 3 - 1 ( đường thẳng)
Vậy với 3 điểm sẽ tạo được số đường thẳng là:
(3-1)\(\times\)3 (đường thẳng)
Theo cách tính trên mỗi đường thẳng được tính hai lần vậy số đường thẳng được tạo là:
( 3-1)\(\times\) 3 : 2 = 3 ( đường thẳng)
Kết luận: Qua 3 điểm không thẳng hàng ta có thể vẽ được 3 đường thẳng

Dùng phương pháp quy nạp toán học em nhé.
Với n = 1 ta có: 41 + 15.1 - 1 = 18 ⋮ 9 ( đúng)
Giả sử 4n + 15n - 1 ⋮ 9 với n = k (kϵ N)
Ta cần chứng minh 4n + 15n - 1 ⋮9 với n = k + 1
⇔ 4k+1 + 15(k+1) - 1 ⋮ 9
Thật vậy ta có:
4k + 15k - 1 ⋮ 9 ( theo giả thuyết)
⇔ 4.( 4k + 15k - 1) ⋮ 9
⇔ 4k+1 + 60k - 4 ⋮ 9
⇔ 4k+1 + 15k + 45k + 15 - 1 - 18 ⋮ 9
⇔ 4k+1 + 15k + 15 - 1+ 45k - 18 ⋮ 9
⇔ 4k+1 + 15(k+1) - 1 + 45k - 18 ⋮ 9
⇔ 4k+1 + 15(k+1) - 1 ⋮ 9 ( đpcm)
Vậy 4n + 15n - 1 ⋮ 9 ∀ n ϵ N

\(\dfrac{-5}{23}\cdot\dfrac{17}{26}+\dfrac{5}{-23}\cdot\dfrac{9}{26}\)
= \(\dfrac{-5}{23}\cdot\dfrac{17}{26}+\dfrac{-5}{23}\cdot\dfrac{9}{26}\)
= \(\dfrac{-5}{23}\left(\dfrac{17}{26}+\dfrac{9}{26}\right)\)
= \(\dfrac{-5}{23}\cdot1=\dfrac{-5}{23}\)

Lời giải:
$=(-7+|13|)-(13-|-7|-25)-(25+|-10|-9)$
$=(-7+13)-(13-7-25)-(25+10-9)$
$=-7+13-13+7+25-25-10+9$
$=(-7+7)+(13-13)+(25-25)-10+9=-10+9=-1$

\(\left(-\dfrac{1}{3}\right)^2\).18-35:33+(-5).4
= \(\dfrac{1}{9}\).18-32+(-5).4
=2-9+(-20)
=-27

A = 1 - \(\dfrac{1}{1.2}\) - \(\dfrac{1}{2.3}-\dfrac{1}{3.4}-\dfrac{1}{4.5}...-\dfrac{1}{97.98}\)
A= 1-\(\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{97.98}\right)\)
A= 1- \(\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}...+\dfrac{1}{97}-\dfrac{1}{98}\right)\)
A= 1- \(\left(\dfrac{1}{1}-\dfrac{1}{98}\right)\)
A=1- 1 + \(\dfrac{1}{98}\)
A= \(\dfrac{1}{98}\)
Lời giải:
$1-A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{97.98}$
$1-A=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{98-97}{97.98}$
$1-A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{97}-\frac{1}{98}$
$=1-\frac{1}{98}$
$\Rightarrow A=\frac{1}{98}$
Lời giải:
Gọi tổng trên là $A$
$A=2(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.11}+...+\frac{1}{100.103})$
$A=\frac{2}{3}(\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.11}+...+\frac{3}{100.103})$
$=\frac{2}{3}(\frac{4-1}{1.4}+\frac{7-4}{4.7}+...+\frac{103-100}{100.103})$
$=\frac{2}{3}(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+....+\frac{1}{100}-\frac{1}{103})$
$=\frac{2}{3}(1-\frac{1}{103})$
$=\frac{2}{3}.\frac{102}{103}=\frac{68}{103}$
Bạn Akai Haruma đáp án của bạn đúng khi phân số 1/7*11 là 1/7*10