A=\(\dfrac{2}{15}\)+\(\dfrac{2}{35}\)+\(\dfrac{2}{63}\)+...+\(\dfrac{2}{399}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`-3/3*15/13-3/7*11/13-3/7`
`-1*15/13-3/7*11/13-3/7`
`=-3/7:3/7*15/13-3/7*11/13-3/7`
`=-3/7*35/13-3/7*11/13-3/7`
`=-(3/7*35/13+3/7*11/13+3/7)`
`=-3/7(35/13+11/13+1)`
`=-3/7*59/13`
`=-177/91`

`1/2+3/5(x-2)=1/5`
`=>3/5(x-2)=1/5-1/2`
`=>3/5(x-2)=2/10 -5/10`
`=>3/5(x-2)=-3/10`
`=> x-2= -3/10 : 3/5`
`=> x-2= -3/10 xx 5/3`
`=> x-2=-1/2`
`=>x=-1/2 +2`
`=>x=-1/2 + 4/2`
`=>x= 3/2`

\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+.....+\dfrac{1}{2021.2023}\)
\(=\dfrac{1}{2}.\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+....+\dfrac{2}{2021.2023}\right)\)
\(=\dfrac{1}{2}.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+....+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}.\left(1-\dfrac{1}{2023}\right)=\dfrac{1}{2}.\dfrac{2022}{2023}=\dfrac{1011}{2023}\)
Ta có A = \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{2021\cdot2023}\)
= \(\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{2021\cdot2023}\right)\)
= \(\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2021}+\dfrac{1}{2023}\right)\)
= \(\dfrac{1}{2}\left(1-\dfrac{1}{2023}\right)=\dfrac{1}{2}\cdot\dfrac{2022}{2023}=\dfrac{1011}{2023}\)

Ta có ( x2 + 1 )( x + 1 ) = 3y
x2( x + 1 ) + x + 1 = 3y
x3 + x2 + x = 3y - 1
x( x2 + x + 1 ) = 3y - 1
Vì 3y ⋮ 3 nên 3y - 1 chia 3 dư 2
Khi đó x chia hết cho 3; x2 + x + 1 chia 3 dư 2 hoặc x chia 3 dư 2; x2 + x + 1 hia hết cho 3
Giả sử x chia hết cho 3 ⇒ x có dạng 3k ( k ϵ N )
Ta được 3k( 3k2 + 3k + 1 )
Vì 3k2 + 3k + 1 chia 3 dư 1 nên 3k( 3k2 + 3k + 1 ) chia 3 dư 1 ( trái với giả thiết ) → loại
Giả sử x chia 3 dư 2 ⇒ x có dạng 3k + 2 ( k ϵ N )
Ta được ( 3k + 2 )[( 3k + 2 )2 + 3k + 2 + 3 ]
( 3k + 2 )[ 9k2 + 12k + 3k + 5 ]
Vì 9k2 + 12k + 3k + 5 chia 3 dư 2 nên ( 3k + 2 )[ 9k2 + 12k + 3k + 5 ] chia 3 dư 1 ( trái với giả thiết ) → loại
Vậy không có x; y nào thỏa mãn ( x2 + 1 )( x + 1 ) = 3y
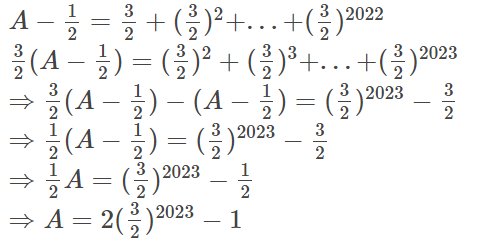

`A =2/15 +2/35 +2/63 +... +2/339`
`= 2/(3.5) +2/(5.7) + 2/(7.9) + ...+2/(19.21)`
`= 1/3 -1/5 +1/5 -1/7 +1/7 -1/9 +... 1/19 -1/21`
`= 1/3 -1/21 = 7/21 -1/21`
`=6/21 = 2/7`
A=2/15+2/35+2/63+...+2/339
=2/(3.5)+2/(5.7)+2/(7.9)+...+2/(19.21)=2/(3.5)+2/(5.7)+2/(7.9)+...+2/(19.21)
=1/3−1/5+1/5−1/7+1/7−1/9+...1/19−1/21=1/3−1/5+1/5−1/7+1/7−1/9+...1/19−1/21
=1/3−1/21=7/21−1/21=1/3−1/21=7/21−1/21
=6/21=2/7=6/21=2/7