Ta có \(\sqrt{2022a+\dfrac{\left(b-c\right)^2}{2}}\) 

\(=\sqrt{2a\left(a+b+c\right)+\dfrac{b^2-2bc+c^2}{2}}\)

\(=\sqrt{\dfrac{4a^2+b^2+c^2+4ab+4ac-2bc}{2}}\)

\(=\sqrt{\dfrac{\left(2a+b+c\right)^2-4bc}{2}}\)

\(\le\sqrt{\dfrac{\left(2a+b+c\right)^2}{2}}\)

\(=\dfrac{2a+b+c}{\sqrt{2}}\).

Vậy \(\sqrt{2022a+\dfrac{\left(b-c\right)^2}{2}}\le\dfrac{2a+b+c}{\sqrt{2}}\). Lập 2 BĐT tương tự rồi cộng vế, ta được \(VT\le\dfrac{2a+b+c+2b+c+a+2c+a+b}{\sqrt{2}}\)

\(=\dfrac{4\left(a+b+c\right)}{\sqrt{2}}\) \(=\dfrac{4.1011}{\sqrt{2}}\) \(=2022\sqrt{2}\)

ĐTXR \(\Leftrightarrow\) \(\left\{{}\begin{matrix}ab=0\\bc=0\\ca=0\\a+b+c=1011\end{matrix}\right.\) \(\Leftrightarrow\left(a;b;c\right)=\left(1011;0;0\right)\) hoặc các hoán vị. Vậy ta có đpcm.

Giá của chiếc tivi sau khi giảm nhân dịp 30/4 là

\(13328000\div\left(100\%-20\%\right)=16660000\) ( đồng )

Giá ban đầu của chiếc tivi llà

\(16660000\div\left(100\%-15\%\right)=19600000\) ( đồng )

(a² + b² + c²).(1+1+1) ≥ (a.1 + b.1 + c.1)² = 1
=> a² + b² + c² ≥ 1/3

dấu "=" xảy ra <=> a/1 = b/1 = c/1 => a = b = c = 1/

Lời giải:

a. Bạn tự vẽ

b. Gọi ptđt $(D)$ là $y=ax+b$. Vì $A\in (D)$ nên:

$y_A=ax_A+b\Leftrightarrow -3=a+b(1)$

$(D)$ tiếp xúc với $(P)$
$\Leftrightarrow$ phương trình hoành độ giao điểm $x^2-ax-b=0$ có nghiệm kép 

$\Leftrightarrow \Delta=a^2+4b=0(2)$

Từ $(1); (2)\Rightarrow a=6$ hoặc $a=-2$
Nếu $a=6$ thì $b=-3-a=-9$. 

Nếu $a=-2$ thì $b=-3-a=-3-(-2)=-1$
Vậy ptđt $(D)$ là $y=6x-9$ hoặc $y=-2x-1$

c. 

PT hoành độ giao điểm của $(d)$ và $(P)$:

$x^2-(2-m)x-(m-1)=0$

Để $(P)$ và $(d)$ cắt nhau tại 2 điểm pb thì:

$\Delta=(2-m)^2+4(m-1)>0\Leftrightarrow m^2>0\Leftrightarrow m\neq 0$

Áp dụng định lý Viet:

$x_1+x_2=2-m$

$x_1x_2=-(m-1)=1-m$

$\Rightarrow x_1x_2-x_1-x_2=-1$

$\Leftrightarrow x_1x_2-x_1-x_2+1=0$

$\Leftrightarrow (x_1-1)(x_2-1)=0$

$\Leftrightarrow x_1=1$ hoặc $x_2=1$

Nếu $x_1=1$

$x_2^3-2x_1=64$

$\Leftrightarrow x_2^3-2=64\Leftrightarrow x_2^3=66$

$\Leftrightarrow x_2=\sqrt[3]{66}$
$2-m=x_1+x_2=1+\sqrt[3]{66}$

$\Leftrightarrow m=1-\sqrt[3]{66}$

Nếu $x_2=1$

$x_2^3-2x_1=64$

$\Leftrightarrow 1-2x_1=64$

$\Leftrightarrow x_1=\frac{-63}{2}$

$2-m=x_1+x_2=\frac{-63}{2}+1=\frac{-61}{2}$

$\Leftrightarrow m=\frac{65}{2}$

Ta thấy \(x>0\) nên ta có thể suy ra \(\sqrt{x}=\sqrt{4-2\sqrt{3}}\) \(=\sqrt{3-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}-1\right)^2}\) \(=\sqrt{3}-1\) (do \(\sqrt{3}-1>0\))

Từ đó \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) \(=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\) \(=\dfrac{\sqrt{3}}{\sqrt{3}-4}\) \(=\dfrac{\sqrt{3}\left(\sqrt{3}+4\right)}{\left(\sqrt{3}-4\right)\left(\sqrt{3}+4\right)}\) \(=\dfrac{3+4\sqrt{3}}{\left(\sqrt{3}\right)^2-4^2}\) \(=-\dfrac{3+4\sqrt{3}}{13}\)

Ta có : \(x\text{=}4-2\sqrt{3}\)

\(\Rightarrow x=3-2\sqrt{3}+1\)

\(\Rightarrow x=\left(\sqrt{3}-1\right)^2\)

\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-1\right)^2}\text{=}\sqrt{3}-1\)

Do đó :

\(Q\text{=}\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(Q\text{=}\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\)

\(Q\text{=}\dfrac{\sqrt{3}}{\sqrt{3}-4}\)

Chắc đến đây thôi nhỉ .

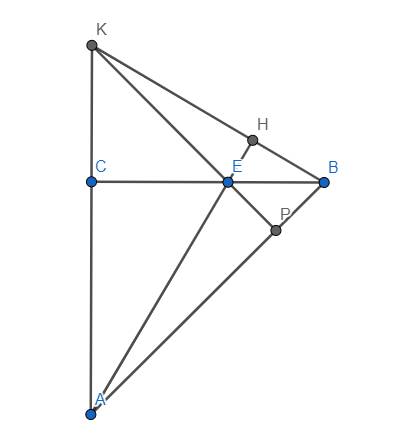
 Do \(CA=CB=a\) nên \(BE.BC+AC.AK=a\left(AK+BE\right)\) 

 Ta chứng minh \(AK+BE\) không đổi. Thật vậy, gọi P là giao điểm của KE và AB. Quan sát thấy E là trực tâm tam giác ABK \(\Rightarrow KP\perp AP\) tại P. Lại có \(\widehat{KAP}=45^o\) nên suy ra \(\widehat{AKP}=45^o\). Từ đó suy ta tam giác CEK cân tại C hay \(CE=CK\). 

 Từ đó \(AK+BE=AC+CK+BC-CE=2a\). Vậy \(BE.BC+AC.AK=2a^2\) không đổi (đpcm)