UCLN4;6=bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\left(\frac{\left(x+1\right)^2.\left(y+1\right)^2}{\left(x+1\right)^2}+\frac{\left(x+1\right)^2\left(y+1\right)^2}{\left(y+1\right)^2}\right)\left(xy+1\right)\ge\left(x+1\right)^2\left(y+1\right)^2\)
\(\left[\left(y+1\right)^2+\left(x+1\right)^2\right]\left(xy+1\right)\ge\left(xy+y+x+1\right)^2\)
\(\left(y^2+2y+1+x^2+2x+1\right)\left(xy+1\right)\ge\left(xy+y+x+1\right)^2\)
\(\left(y^2+2y+1+x^2+2x+1\right)\left(xy+1\right)-\left(xy+y+x+1\right)^2\ge0\)
\(\left(y^2+2y+1+x^2+2x+1\right)\left(xy+1\right)-\left(x^2+2x+1\right)\left(y^2+2y+1\right)\ge0\)
\(xy\left(x-1\right)^2+\left(xy-1\right)^2\ge0\)
\(< =>BĐT\)luôn đúng
dấu "=" xảy ra khi \(x=y=1\)
mình ko chắc đã đúngg đâu

ĐK: \(x^2-3y^2+30\ge0\).
Phương trình thứ nhất tương đương với:
\(\left(x-y+3\right)\left(x+2y-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=y-3\\x=1-2y\end{cases}}\)
Với \(x=y-3\)thế vào phương trình thứ hai ta được:
\(\sqrt{\left(y-3\right)^2-3y^2+30}+y-3-2y-5=0\)
\(\Leftrightarrow\sqrt{-2y^2-6y+39}=y+8\)
\(\Rightarrow-2y^2-6y+39=y^2+16y+64\)
\(\Leftrightarrow\orbr{\begin{cases}y=\frac{-11+\sqrt{46}}{3}\Rightarrow x=\frac{-20+\sqrt{46}}{3}\\y=\frac{-11-\sqrt{46}}{3}\Rightarrow x=\frac{-20-\sqrt{46}}{3}\end{cases}}\)
Thử lại thỏa mãn.
Với \(x=1-2y\)làm tương tự, thu được thêm một nghiệm là: \(x=\frac{17-2\sqrt{61}}{5},y=\frac{-6+\sqrt{61}}{5}\).


ĐK: \(1-sinx\ne0\Leftrightarrow x\ne\frac{\pi}{2}+l2\pi\left(l\inℤ\right)\).
\(\frac{cos3x}{1-sinx}=0\)
\(\Rightarrow cos3x=0\)
\(\Leftrightarrow3x=\frac{\pi}{2}+k\pi\left(k\inℤ\right)\)
\(\Leftrightarrow x=\frac{\pi}{6}+\frac{k\pi}{3}\left(k\inℤ\right)\)
Đối chiếu điều kiện:
\(\frac{\pi}{6}+\frac{k\pi}{3}=\frac{\pi}{2}+l\pi\Leftrightarrow\frac{1}{3}=\frac{k}{3}-l\Leftrightarrow k=3l+1\).
Vậy nghiệm phương trình là \(x=\frac{\pi}{6}+\frac{k\pi}{3}\)với \(k\inℤ,k\ne3l+1\left(l\inℤ\right)\).

bạn vẽ trục số ra thì ra đc
\(-1\le x\le2\)
kết luận.......

Câu 1:
\(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-sin^2x=1-\left(\frac{4}{5}\right)^2=\frac{9}{15}\)
\(\Leftrightarrow cos^2x=\frac{\pm3}{5}\).
Câu 2:
Đường tròn \(\left(C\right)\)có tâm \(I\left(2,-1\right)\)bán kính \(R=\sqrt{25}=5\).
Gọi \(d\)là tiếp tuyến của đường tròn \(\left(C\right)\)tại điểm \(M\). Khi đó \(IM\)và \(d\)vuông góc với nhau.
\(\Rightarrow\overrightarrow{IM}=\left(3,4\right)\)là một vector pháp tuyến của \(d\)
Suy ra phương trình \(d:3\left(x-5\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-27=0\).
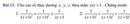
Ta có :
4 = 22
6 = 2 . 3
=> ƯCLN ( 4 ; 6 ) = 2
Vậy ƯCNN ( 4 ; 6 ) = 2
đáp án
ucln của 4 và 6 là
2