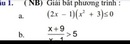tìm điều kiện của bất phương trình: a/![]() b/
b/ ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(AJ=\frac{1}{2}\left(AH+AC\right)\)
\(BI=\frac{1}{2}\left(BA+BH\right)\)
\(AJ.BI=\frac{1}{4}\left(AH+AC\right)\left(BA+BH\right)\)
\(=\frac{1}{4}\left(AH.BA+AH.BH+AC.BA+AC.BH\right)\)
\(=\frac{1}{4}\left(AH.HA+0+0+HC.BH\right)\)
\(=\frac{1}{4}\left(-AH^2+BH.HC\right)\)
Mà: Tam giác ABC vuông tại A <=> \(AH^2=HC.HB\)
Vậy \(AJ.BI=0\Leftrightarrow AJ\perp BI\)


\(a,f\left(x\right)=\frac{x}{\sqrt{4-x}}\)
\(ĐKXĐ:4-x>0< =>x< 4\)
\(TXĐ:D=\left(4;-\infty\right)\)
ta có \(-5\in D\)nhưng \(5\notin D\)
hs ko chẵn cũng ko lẻ
\(b,f\left(x\right)=\sqrt{2x-1}+\sqrt{1+2x}\)
\(ĐKXĐ:x\ge\frac{1}{2};x\ge-\frac{1}{2}< =>x\ge\frac{1}{2}\)
\(TXĐ:D=[\frac{1}{2};+\infty)\)
bạn biện luận như câu trên thì ra đc hàm số ko chẵn cũng ko lẻ
\(c,f\left(x\right)=\sqrt{x-2}+\frac{1}{2+x}\)
\(ĐKXĐ:x\ge2;x\ne-2< =>x\ge2\)
\(D=[2;+\infty)\)
ta có \(3\in D\)nhưng \(-3\notin D\)nên hàm số ko chẵn cũng ko lẻ
\(d,f\left(x\right)=\left|2x-3\right|-\left|2x+3\right|\)
\(TXĐ:D=|R\)
\(\forall x\in D< =>-x\in D\)
\(-f\left(x\right)=\left|-2x-3\right|-\left|-2x+3\right|\)
\(-f\left(x\right)=\left|-\left(2x+3\right)\right|-\left|-\left(2x-3\right)\right|\)
\(-f\left(x\right)=\left|2x+3\right|-\left|2x-3\right|\)
\(-f\left(x\right)=-\left(-\left|2x+3\right|+\left|2x-3\right|\right)\)
\(-f\left(x\right)=-\left(\left|2x-3\right|-\left|2x+3\right|\right)=f\left(-x\right)\)
hàm số lẻ
hai câu còn lại cậu làm nốt hen

Ta có: \(a,b\)không chia hết cho \(3\)do đó \(a^2\equiv1\left(mod3\right),b^2\equiv1\left(mod3\right)\).
\(a^2-b^2=\left(a^2-1\right)-\left(b^2-1\right)\).
Ta sẽ chứng minh \(a^2-1⋮24\).
\(24=3.8,\left(3,8\right)=1\)do đó ta sẽ chứng minh \(a^2-1\)chia hết cho \(3\)và \(8\).
- \(a^2-1⋮3\)chứng minh trên.
\(a^2-1=\left(a-1\right)\left(a+1\right)\)là tích của hai số chẵn liên tiếp nên có một thừa số chia hết cho \(2\)(nhưng không chia hết cho \(4\)), một thừa số chia hết cho \(4\)do đó chia hết cho \(2.4=8\).
Tương tự với \(b^2-1\).
Do đó ta có đpcm.

\(\hept{\begin{cases}x+m\le0\\-x+5< 0\end{cases}\hept{\begin{cases}x\le-m\\x< -5\end{cases}\hept{\begin{cases}x\in\left(-\infty;-m\right)\\x\in\left(-\infty;-5\right)\end{cases}}}}\)bạn sửa lại chỗ trên nha là nửa khoảng
\(+-m\ge-5\)
\(m\le5< =>\)tập nghiệm của HPT \(S=\left(-m;-\infty\right)\)
\(+-m< 5\)
\(m>5< =>\)tập nghiệm của HPT \(S=\left\{-\infty;-5\right\}\)

a. ta có \(x^2+3>0\text{ nên }\left(2x-1\right)\left(x^2+1\right)\le0\Leftrightarrow2x-1\le0\Leftrightarrow x\le\frac{1}{2}\)
b. ta có \(\frac{x+9}{x-1}>5\Leftrightarrow\frac{x+9-5x+5}{x-1}>0\Leftrightarrow\frac{14-4x}{x-1}>0\)
\(\hept{\begin{cases}14-4x>0\\x-1>0\end{cases}\Leftrightarrow\frac{7}{2}>x>1}\) hoặc \(\hept{\begin{cases}14-4x< 0\\x-1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>\frac{7}{2}\\x< 1\end{cases}}}\) vô lí
vậy \(1< x< \frac{7}{2}\)
a) \(\left(2x-1\right)\left(x^2+3\right)\le0\)
\(\Leftrightarrow\hept{\begin{cases}2x-1\le0\\x^2+3\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2x-1\ge0\\x^2+3\le0\end{cases}}\)
mà \(x^2+3>0\forall x\)
nên \(\hept{\begin{cases}2x-1\le0\\x^2+3>0\end{cases}}\)
\(\Leftrightarrow x\le\frac{1}{2}\)
Vậy nghiệm của BPT là \(x\le\frac{1}{2}\)
b) Đề bị che mất mẫu số nên không đọc được đề =))